Algebra dei limiti
Esistono alcune regole relative alle operazioni aritmetiche che possono essere eseguite sui limiti; supponendo che i limiti di cui ora parleremo esistano e siano finiti valgono i seguenti teoremi:
Date le funzioni y=f(x) e y=g(x) se
![]() ed
ed ![]() allora
si ha:
allora
si ha:
1 Il limite della somma di due funzioni è uguale alla somma dei limiti
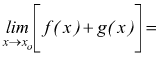
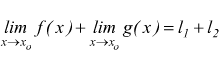
2 La differenza di due funzioni ha per limite la differenza dei limiti
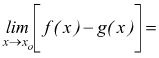
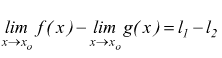
Più in generale, il limite della somma algebrica di quante si vogliano funzioni è uguale alla somma algebrica dei limiti.
3 Il limite del prodotto di una costante per una funzione è uguale al prodotto della costante per il limite della funzione
![]()
in base a questo teorema si conclude che se f(x) e g(x) sono due funzioni che per x→xo ammettono come limiti rispettivamente l1 ed l2 e se k ed h sono due costanti, allora si ha

cioè, il limite di una combinazione lineare di funzioni è la combinazione lineare dei limiti. Per questo motivo si dice che il limite è un operatore lineare.
4 Il limite del prodotto di due funzioni è uguale al prodotto dei limiti delle due funzioni.
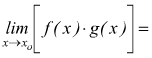

Più in generale si può affermare che il limite del prodotto di più funzioni
è uguale al prodotto del limite delle singole funzioni.
In particolare, se uno dei fattori tende a zero e gli altri ad un limite
finito, il prodotto tende a zero. Cioè se
![]()
![]()
allora si ha ![]()
Se, invece, uno dei fattori tende ad infinito e l'altro ad un limite finito diverso da zero, il prodotto tende all'infinito e per il segno vale la solita regola dei segni
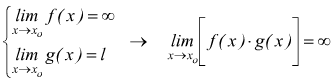
per il momento non possiamo dire niente quando uno dei fattori tende all'infinito e l'altro tende a zero, generando la forma di indecisione 0·∞.
Una conseguenza di questo teorema è il seguente corollario:
Il limite della potenza con esponente intero n positivo di una funzione che tende ad un limite finito à la potenza n-esima del limite:
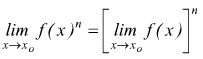
5 Se per x→xo ,f(x) tende al
limite finito l≠0 la funzione ![]() tende
sempre per x→xo al limite
tende
sempre per x→xo al limite ![]() .
Quindi se
.
Quindi se
 in
particolare si ha, se
in
particolare si ha, se

6 Il limite del quoziente di due funzioni è uguale al quoziente dei limiti delle due funzioni.
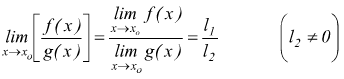
Forme indeterminate
Le regole di calcolo elencate in precedenza sulle operazioni di somma
algebrica, prodotto e divisione tra limiti rimangono valide per x che tende
sia a valori finiti che infiniti; cioè per
![]()
![]()
Somma di funzioni
Considerando sempre il valore del limite l un numero reale finito (anche
zero)

come si vede l'ultimo caso porta ad una forma di indecisione del tipo +∞-∞.
Prodotto di funzioni
Con l numero finito e diverso da zero.
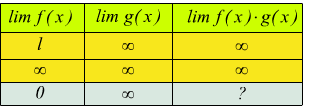
anche in questo caso è presente una forma di indecisione 0·∞.
Quoziente di funzioni
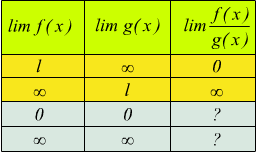
vengono messe in evidenza due forme di indeterminazione ![]() e
e
![]() .
.
Esponenziale
Si tratta, in questo caso di considerare il limite della potenza ![]() tenendo
presente che è
tenendo
presente che è
![]()
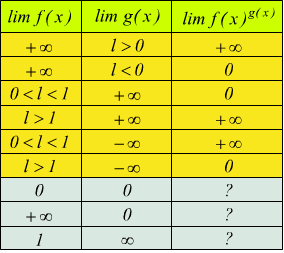
vengono individuate tre forme di indeterminazione 00 con ∞0 ed infine 1∞ : in totale abbiamo sette forme di indeterminazione.
Dobbiamo tener presente che le forme di indeterminazione riscontrate non significano l'assenza del limite, ma rivelano la mancanza di una relazione con il limite delle singole funzioni. Per trovare il limite, occorre, in genere elaborare ulteriori calcoli.
Forma +∞–∞
Come situazione di riferimento possiamo prendere una qualsiasi funzione polinomiale del tipo
![]()
dove ao , a1 , ... , an-1 , an sono numeri reali. Quando x tende a +∞ o a -∞ ci possono essere due casi
a Tutti gli addendi (escluso an)
tendono a +∞ o a -∞ per cui l'intero polinomio tende rispettivamente
a +∞ o a -∞.
b Alcuni addendi tendono a +∞ e
altri a -∞ e qui si presenta la forma di indeterminazione +∞-∞.
Quando è possibile si effettua il seguente artificio: si raccoglie a fattor
comune la potenza di esponente maggiore xn.
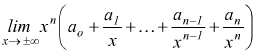
tutti i termini dentro la parentesi tonda, eccetto il primo tenderanno a zero, per cui il limite del polinomio, per x che tende a +∞ o a -∞ è dato dal limite del suo termine di grado maggiore.
esempio ![]()
osserviamo che il limite assegnato si presenta in forma indeterminata +∞-∞
ma come si può dedurre da questo esempio il limite x→∞ di un
polinomio, è sempre infinito ed il segno dipende dal termine del polinomio
che ha il grado massimo.

Nel passaggio (1) abbiamo raccolto a fattor comune la massima potenza di x; nel passaggio (2) abbiamo applicato il teorema sul limite del prodotto; nel passaggio (3) il teorema sul limite di una potenza e quello sul limite di una differenza.
esempio
![]()
Si tratta, evidentemente, di un caso di indecisione +∞-∞ e
in questo caso si ricorre ad un artificio in modo che si possa riscrivere
la funzione senza che essa abbia al numeratore la differenza ![]() cioè
moltiplichiamo e dividiamo la funzione per che
cioè
moltiplichiamo e dividiamo la funzione per che ![]() equivale
a moltiplicare la funzione per 1 (cioè la lascia invariata)
equivale
a moltiplicare la funzione per 1 (cioè la lascia invariata)
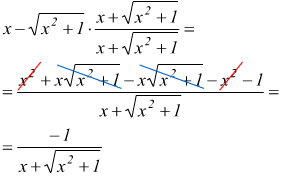
dunque

Forma ∞/∞
Si presenta frequentemente nel caso di funzioni razionali fratte del tipo
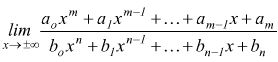
dove ao , a1 , ... , am , bo
, b1 , ... , bn costanti reali ao≠0
, bo≠0 , m≥1 , n≥1.
Quando in questa forma si ha x tende a +∞ oppure a -∞ si ha
la forma di indeterminazione ∞/∞.
La forma di indeterminazione può essere eliminata, in questo caso raccogliendo
xm al numeratore ed xn al denominatore.

qui ci possono essere tre casi
a m>n
![]() mentre
mentre
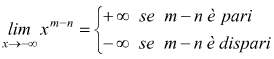
poi dipende dal segno del rapporto ![]()
b m=n
![]()
di conseguenza, il limite richiesto vale ![]()
c m<n
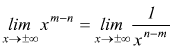 essendo
n-m>0 si ha
essendo
n-m>0 si ha ![]()
esempio
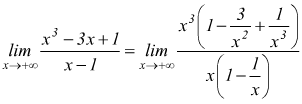
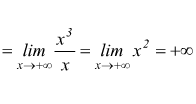
esempio
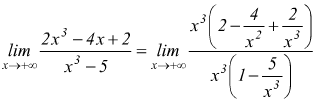

esempio
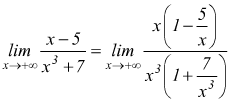

Forma 0/0
Anche in questo caso bisogna ricorrere a manipolazioni della funzione espressa nella scrittura di limite; nel caso frequente di funzioni razionali fratte si cerca di scomporre il polinomio al numeratore e quello al denominatore, ad esempio:
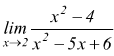
Il limite si presenta sotto la forma ![]() .
Numeratore e denominatore si annullano per x=2,per cui sono divisibile per
(x-2); tenendo presente che interessa il comportamento della funzione per
x≠2 scriveremo
.
Numeratore e denominatore si annullano per x=2,per cui sono divisibile per
(x-2); tenendo presente che interessa il comportamento della funzione per
x≠2 scriveremo
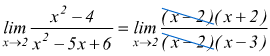

Nel caso si debba operare con limiti di funzioni trigonometriche può essere
utile conoscere il limite notevole ![]() .
.
Limite notevole sinx/x
Il calcolo del limite 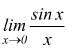 dove
x è la misura dell'arco in radianti che tende a zero, presenta la forma
di indecisione
dove
x è la misura dell'arco in radianti che tende a zero, presenta la forma
di indecisione ![]() .
Osservando il disegno del cerchio trigonometrico di raggo 1, si riconosce
per analogia geometrica
.
Osservando il disegno del cerchio trigonometrico di raggo 1, si riconosce
per analogia geometrica

Chiamiamo PA la lunghezza dell'arco di circonferenza tra P ed A, avremo evidentemente
![]()
Per la geometria, la lunghezza dell'arco è ![]() ma
nel cerchio trigonometrico r = 1, dunque:
ma
nel cerchio trigonometrico r = 1, dunque:
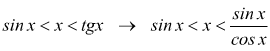 dividendo
tutto per sinx
dividendo
tutto per sinx
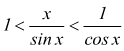 invertendo
invertendo
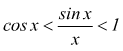
ora, sapendo che è ![]() e
e
![]() per
il teorema del confronto la funzione
per
il teorema del confronto la funzione ![]() è
compresa tra le due funzioni y=cosx e y=1; quindi deve essere
è
compresa tra le due funzioni y=cosx e y=1; quindi deve essere
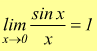
inoltre, il limite ![]() permette
l'introduzione di un nuovo limite notevole.
permette
l'introduzione di un nuovo limite notevole.
Limite notevole 1-cosx/x
Il limite 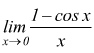 presenta,
apparentemente, forma di indeterminazione
presenta,
apparentemente, forma di indeterminazione ![]() ;
ma se moltiplichiamo e dividiamo per 1+cosx l'espressione sotto il segno
di limite, otteniamo
;
ma se moltiplichiamo e dividiamo per 1+cosx l'espressione sotto il segno
di limite, otteniamo
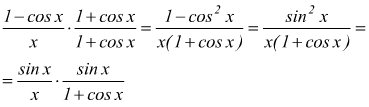
per il teorema del prodotto dei limiti 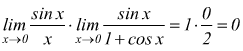 si
conclude che è:
si
conclude che è:

Limite notevole 1-cosx/x2
Il limite 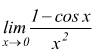 presenta
forma di indeterminazione
presenta
forma di indeterminazione ![]() .
Applicando il ragionamento precedente abbiamo
.
Applicando il ragionamento precedente abbiamo
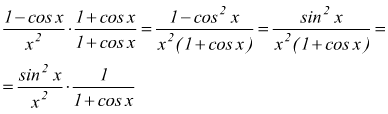
per il teorema del prodotto dei limiti 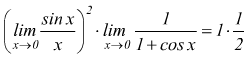 dunque
dunque
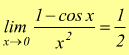
Limite notevole del numero di Nepero
E' possibile dimostrare che la successione
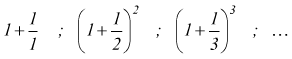
che ha termine generale 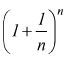 è
convergente ad un numero irrazionale compreso tra 2 e 3. Questo limite si
chiama numero di Nepero e si indica con
la lettera "e". Quindi si ha:
è
convergente ad un numero irrazionale compreso tra 2 e 3. Questo limite si
chiama numero di Nepero e si indica con
la lettera "e". Quindi si ha:

Il numero "e" è stato assunto da Nepero come base di un sistema di logaritmi,
detti appunto Neperiani o logaritmi naturali, che negli sviluppi teorici
sono generalmente preferibili a quelli decimali, usati invece nelle applicazioni
a carattere pratico. E' consuetudine indicare un logaritmo neperiano senza
indicare la base. Il logaritmo neperiano di x viene indicato come log
x o più frequentemente ln x.
Anche per i logaritmi decimali si omette la base e si adopera la maiuscola
nella lettera iniziale del logaritmo come Log x. (N.D.R. nelle pagine
di questo sito il logaritmo neperiano viene sempre indicato ln x,
mentre il logaritmo decimale lg x, perché così abbiamo deciso).
Consideriamo ora la funzione
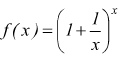
essa ha per campo di esistenza l'insieme dei numeri reali che soddisfano la condizione
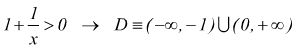
dunque, se x tende a +∞ o a -∞ il limite della funzione è ancora "e".

Limite notevole del numero di logaritmo naturale
Anche il limite 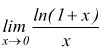 presenta
forma di indeterminazione
presenta
forma di indeterminazione ![]() .
Manipolando l'espressione sotto il segno di limite, utilizzando le proprietà
dei logaritmi:
.
Manipolando l'espressione sotto il segno di limite, utilizzando le proprietà
dei logaritmi:
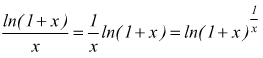
Per la continuità della funzione logaritmica il limite originario può essere riscritto come
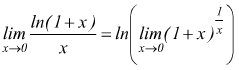
ora poniamo ![]() e
e ![]() con t→∞ quando x→0.
con t→∞ quando x→0.
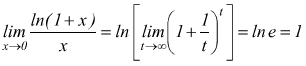 dunque
dunque
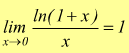
Più in generale è possibile dimostrare se a>0 e a≠1
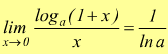 di
cui il limite precedente è evidentemente un caso particolare.
di
cui il limite precedente è evidentemente un caso particolare.
Limite notevole della funzione esponenziale
Il limite  presenta
forma di indeterminazione
presenta
forma di indeterminazione ![]() .
Anche in questo caso precediamo per sostituzione ponendo
.
Anche in questo caso precediamo per sostituzione ponendo

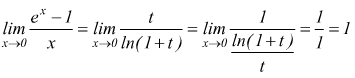
questo per il teorema 5 sulla funzione reciproca; dunque
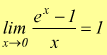
Più in generale è possibile dimostrare se a>0 e a≠1
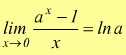
Limite notevole della potenza con differenza
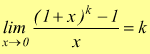 con
k∈R
con
k∈R
Si pone ![]() da cui
da cui
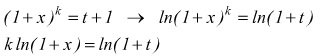
dunque 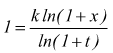 poi, notiamo che t→0 per x→0, cioè:
poi, notiamo che t→0 per x→0, cioè:
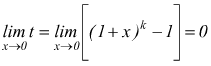 quindi
quindi
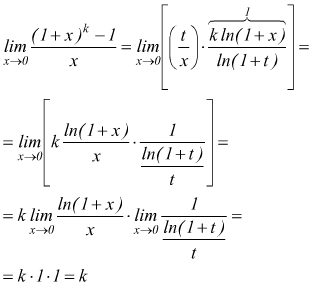
 edutecnica
edutecnica