Iperbole
L’iperbole è il luogo dei punti di un piano per i quali è costante la differenza delle distanze da due punti fissi chiamati fuochi.
Indichiamo i due fuochi come F1 ed F2 e con P(x;y)
il generico punto appartenente alla curva (l’iperbole) di coordinate x ed
y.
Se chiamiamo 2a (con a>0) la differenza costante delle distanze di P
da F1 e da F2 ,avremo
PF1-PF2=2a se PF1>PF2
PF2-PF1=2a se PF1<PF2
in ogni caso sarà ![]() ❶
❶
Chiamiamo F1F2=2c (c>0) distanza focale. La distanza focale è costante perché F1 ed F2 sono due punti fissi.
Per semplicità pensiamo, inizialmente, ad una curva che abbia come assi di simmetria l'asse x e l'asse y e come centro di simmetria l'origine degli assi, l'iperbole definita in questo modo viene detta riferita al centro e ai suoi assi oppure più semplicemente viene chiamata iperbole riferita ai propri assi.
Equazione canonica dell'ellisse con i fuochi sull'asse x
Facciamo l'ipotesi che i due fuochi F1 ed F2 si trovino sull'asse x mentre l'origine O(0;0) coincida con il punto medio del segmento F1F2 .
Se abbiamo indicato con 2c la distanza focale è 
indicando poi con P(x;y) il generico punto di coordinate x ed y appartenente all'iperbole la formula ❶ può essere specificata come
![]()
elevando al quadrato i due membri dell'uguaglianza e svolgendo i calcoli si arriverebbe alla relazione
![]() ❷
❷

se ora si osserva il triangolo F1PF2 si vede che il lato F2F1=2c è più grande sella differenza |PF1-PF2|=2a degli altri due lati (altrimenti non sarebbe un triangolo, dove ogni lato è maggiore della differenza degli altri due) quidi deve essere necessariamente 2c>2a cioè c>a; questo implica che c2-a2>0 sempre. Poniamo:
![]() ❸
❸
in base alla ❸ l'equazione❷ diventa
![]()
 ❹
❹
l'equazione ❹ è l'equazione canonica dell'iperbole in forma normale. Dalla ❸ si ha c2=a2+b2 avendo ipotizzato c>0 si deducono le coordinate dei due fuochi.
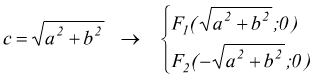
inoltre si osserva che se un punto P(x;y) appartenente all'iperbole di
equazione ❹ allora anche i punti di coordinate (-x;y) (x;-y) e (-x;-y)
appartengono a tale curva; questo vuol dire che la curva è simmetrica rispetto
all'asse x, all'asse y e all'origine .
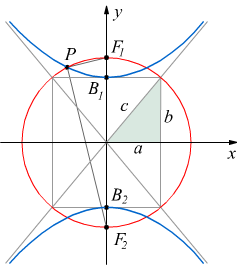
Gli assi cartesiani sono assi di simmetria per l'iperbole mentre l'origine
è il centro di tale simmetria; queste sono le caratteristiche dell'iperbole
riferita al centro e agli assi che può essere rappresentata come si vede
nel disegno.

se nell'equazione canonica dell'iperbole si pone y=0 rappresentativa dell'asse x delle ascisse otteniamo
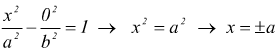
cioè l'asse delle ascisse interseca l'ellisse nei punti  che
vengono chiamati vertici dell'ellisse.
che
vengono chiamati vertici dell'ellisse.
Per questo motivo si dà il nome di asse traverso sia all'asse x che al
segmento A1A2 di misura 2a mentre a viene chiamato
semiasse traverso.
Se adesso cerchiamo di trovare l'intersezione con l'asse y, cioè ponendo
a sistema
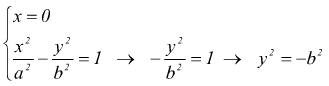
che è impossibile, quindi, l'iperbole non interseca l'asse y. L'asse y si dice asse non traverso.
Asintoti dell'iperbole
L'iperbole è caratterizza da una coppia di asintoti, cioè, due linee retta
alle quali la curva, progressivamente , si avvicina senza mai toccarle.
Per l'iperbole riferita al centro e agli assi hanno equazione
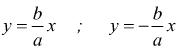

tenendo conto che per l'iperbole
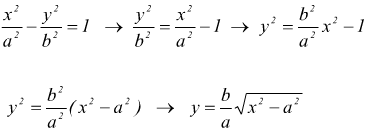
prendiamo un punto P(x;y) appartenente all'iperbole e poi consideriamo il punto Q(x;yo) che ha la stessa ascissa di P e che appartiene all'asintoto che attraversa il primo quadrante la distanza PQ sarà
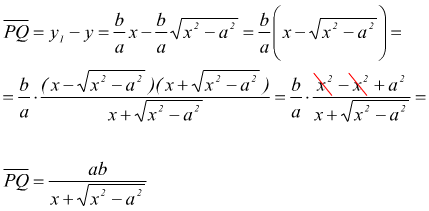
è evidente che all'aumentare di x il valore di questa distanza diminusce progressivamente tendendo a zero. In altri termini la distanza PQ tende a zero al tendere di x all'infinito.
Riassumiamo i parametri fondamentali dell'iperbole riferita al centro e agli assi con i fuochi sull'asse x :

Iperbole con i fuochi sull'asse y
L'iperbole riferita al centro e agli assi di simmetria può anche avere
i fuochi sull'asse y.
L'asse y delle ordinate può contenere i fuochi e quindi può costituire l'asse
traverso mentre l'asse x, sarebbe in questo caso l'asse non traverso. Ripetendo
i procedimenti visti prima, questa configurazione può essere sintetizzata
dalle seguenti formule.

Eccentricità dell'iperbole
L'eccentricità di una iperbole, indicata con e, è il rapporto tra la distanza focale e la misura dell'asse traverso

se i fuochi sono sull'asse x si ha 
![]()
se invece i fuochi sono sull'asse y si ha 
![]()
sappiamo che nell'iperbole la distanza focale c è sempre maggiore della misura dell'asse traverso dunque sarà sempre
![]()
nel caso dell'iperbole, l'eccentricità è una misura dell'apertura dei suoi rami.

Iperbole equilatera
Se nell'equazione canonica risulta essere a=b cioè se i due semiassi traverso e non traverso hanno la stessa lunghezza, l'iperbole si dice equilatera.
Più in generale, un'iperbole si dice equilatera quando i suoi asintoti sono perpendicolari tra di loro, questo fatto implica che i due semiassi traverso e non traverso hanno la stessa lunghezza. Solo in questo caso, infatti, il rettangolo ideale che ha lati pari all'asse traverso e all'asse non traverso passante sui vertici diventa un quadrato
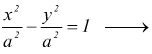
![]()
le equazioni degli asintoti diventano 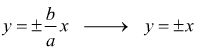
la semidistanza focale diventa ![]()
i vertici dell'iperbole sono i fuochi sono
i fuochi sono 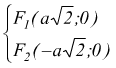
anche se bisogna differenziare a secondo del tipo di iperbole come si vede nei disegni.


Iperbole equilatera riferita ai propri asintoti
Considerando una iperbole equilatera riferita al centro e agli assi di simmetria
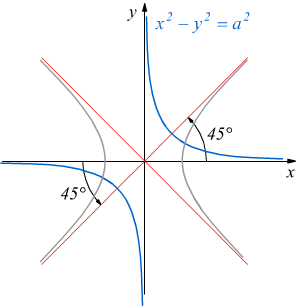
dove l'iperbole disegnata in grigio ha i fuochi sull'asse x. Se sottoponiamo
i punti del piano ad una rotazione di 45° in senso orario, oppure antiorario
attorno all'origine O gli asintoti dell'iperbole vengono a coincidere con
gli assi cartesiani (iperbole blu).
Per questo motivo si dice che, in questo caso, l'iperbole è riferita ai
propri asintoti. In questo caso, è possibile dimostrare che l'equazione
.
![]() diventa
diventa
![]() con
con
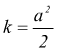 dunque
per l'iperbole equilatera riferita a i propri asintoti si ha
dunque
per l'iperbole equilatera riferita a i propri asintoti si ha
![]() con
k costante che può essere positiva o negativa
con
k costante che può essere positiva o negativa

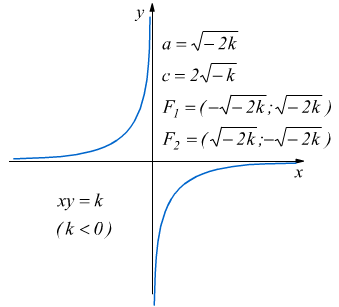
l'iperbole riferita agli asintoti non ha nessun punto di ascissa nulla (x≠0 ∀x) la sua equazione può essere scritta come
![]()
il dominio di una funzione di questo tipo, coincide con l'intero insieme dei numeri reali escluso lo zero D=R-{0}.
k (shift+drag per zoommare)
Funzione omografica
La funzione omografica ha equazione
 con
le condizioni c≠0 e ad-bc≠0 il suo diagramma è il seguente
con
le condizioni c≠0 e ad-bc≠0 il suo diagramma è il seguente

si tratta di una iperbole equilatera con gli asintoti paralleli agli assi cartesiani traslata rispetto a questi.
La traslazione della funzione è definita da 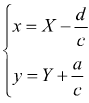
questo porta il punto di origine O(0;0) al punto  sostituendo
nella relazione
sostituendo
nella relazione
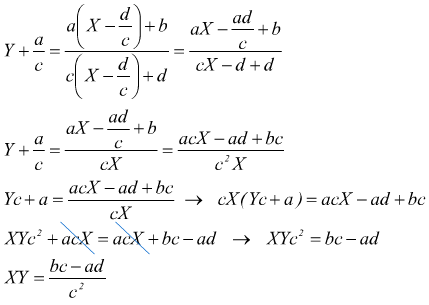
a
b
c
d
(solo numeri interi)
 edutecnica
edutecnica