Funzioni matematiche
Se fissiamo una retta dotata di una freccia, indicatrice di un orientamento
positivo ed un punto (0) su questa, stabiliamo una unità di misura, può
essere già intuitivo associare ad ogni numero reale un corrispondente
punto sulla retta (e viceversa).
Esiste, dunque una corrispondenza biunivoca fra i numeri reali e i punti
di una retta. Una qualsiasi posizione sulla retta viene identificata da
un numero reale x.
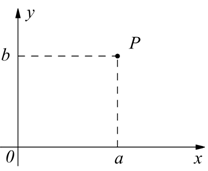
![]()
In tal modo al numero ![]() corrisponde
nel sistema assegnato il punto P indicato in figura e viceversa.
corrisponde
nel sistema assegnato il punto P indicato in figura e viceversa.
In analogia possiamo pensare di individuare un punto in un piano
usando due rette orientate, invece che una. Due rette così definite,
costituiscono un sistema di assi cartesiani ortogonali.
Ogni punto
P del piano ha una unica proiezione (a) sull'asse orizzontale e
(b) su quello verticale, in tal modo si viene a stabilire una corrispondenza
biunivoca fra ciascun punto P del piano ed una coppia (x,y) di numeri
reali.
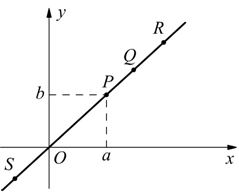
Dopo aver visto come identificare tutti i punti di un piano, ci si potrebbe chiedere come individuare tutti i punti di una linea retta (che assumiamo per semplicità inclinata di 45° rispetto l'asse orizzontale).
Si osserva come ognuno dei punti appartenenti alla retta viene sempre individuato da una coppia (x,y) di numeri reali, ma in questo caso le infinite coppie che rappresentano gli infiniti punti, non possono essere indipendenti fra loro, dato che fra tutti i punti del piano si devono considerare solo quelli appartenenti alla retta.
Ma qual è la relazione che lega insieme questi punti?
Come si vede dalla figura tutti i punti appartenenti alla retta hanno
l'ascissa uguale all'ordinata (a=b). Allora gli infiniti punti della retta
sono tali per cui y=x.
Assegnando un valore arbitrario ad x si ottiene il corrispondente valore
di y.
Se ci ponessimo la domanda contraria , cioè data la regola di dipendenza
y=x, qual è la linea che la rappresenta.
La risposta sarebbe semplice: fissata una coppia di assi cartesiani ortogonali
ed una unità di misura bisogna considerare tutti quei punti che sul piano
hanno l'ordinata uguale all'ascissa.
Poniamoci ora il problema che la relazione fra x ed y sia :
![]()
è il problema di trovare solo quei punti del piano le cui ordinate sono
date dal quadrato delle corrispondenti ascisse, diminuito del triplo dell'ascissa
stessa.
Allora daremo dei valori arbitrari alla x determinando il corrispondente
valore di y; poi rappresentiamo le coppie ottenute sul piano cartesiano
congiungendo con una linea continua i punti ottenuti.

|
x
|
0
|
1
|
-1
|
2
|
-2
|
3
|
-3
|
40
|
|
y
|
0
|
-2
|
4
|
-2
|
10
|
0
|
18
|
4
|
A questo punto è evidente che
● tutti i punti del piano sono individuati
da coppie di numeri reali
● se fra le coordinate (x,y) dei punti c'è
una dipendenza, questa si traduce in una linea, grafico (o diagramma) sul
piano cartesiano.
● al variare del tipo di dipendenza,
varia la forma del grafico. Implicitamente si nota che la dipendenza fra
y ed x si traduce in una sequenza di operazioni fatte sulla x per ottenere
y.
Se considerassimo
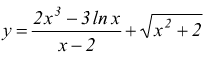
le operazioni eseguite sulla x sono, potenze somme, sottrazioni, prodotti,
divisioni, logaritmi etc.
Quindi, se si volesse generalizzare il ragionamento , indichiamo col simbolo
f l'insieme di tutte queste operazioni e con y=f(x) la dipendenza fra la
y variabile dipendente) e la x (variabile indipendente). L'espressione y=f(x)
è detta 'funzione di x' e si legge "y uguale ad f di x".
Alle domande: che cos'è una variabile indipendente? Cos'è una funzione?
Si può rispondere:
● Una variabile indipendente (indicata di
solito con la lettera x) è una quantità alla quale si può dare un valore
numerico qualunque.
● Se una quantità y,dipende da x in modo
che ad ogni valore di x corrisponda un valore di y si dice che y è funzione
di x e si scrive y=f(x) oppure y=y(x).
Rappresentazione geometrica di funzioni
Una funzione può essere assegnata
I) tramite la sua espressione analitica.
II) tramite la sua rappresentazione geometrica.
La rappresentazione geometrica dà una idea più immediata del modo che
ha la y di variare al variare della x. Lo scopo dello studio di una funzione
è quello di rappresentare la funzione con un grafico sul piano cartesiano,
quando essa viene data nella sua forma analitica.
Allora è molto semplice. Basta calcolare il valore della y per molteplici
(ma proprio molteplici) valori di x. Se pensiamo alla funzione:
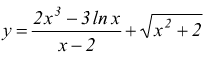
si capisce subito che questo metodo "diretto" o "per punti" non è molto conveniente, si devono eseguire troppe operazioni con spreco di tempo e pericolo di errori. Si preferisce, invece, usare un metodo "indiretto" o "qualitativo", cioè, si ricercano alcune caratteristiche salienti delle funzioni, che, considerate nel loro insieme restituiscono il grafico cercato. Nello studio di una funzione si eseguono le ricerche di queste caratteristiche peculiari in modo sistematico secondo la seguente procedura:
| Caratteristiche | Procedura |
| Campo di esistenza (C.E.) | Dipende dal tipo di funzione |
| Intersezione con gli assi | Si pone x=0 ed y=0 |
| Segno della funzione | Si pone y>0 |
| Condizioni agli estremi del campo | Si determinano con i limiti agli estremi |
| Tratti crescenti e decrescenti | Si studia la derivata prima |
| Punti di massimo o di minimo relativo | Si studia la derivata prima |
| Direzione della tangente in punti particolari | Si calcola la derivata prima nell'intorno di questi |
| Punti di flesso | Si studia la derivata seconda |
| Asintoti obliqui | Si studia la derivata prima per x —>∞ |
Funzioni reali a variabile reale
Le funzioni per le quali è richiesta la rappresentazione grafica possono essere suddivise nelle seguenti categorie:
1 Razionali intere
2 Razionali fratte
3 Irrazionali
4 Sinusoidali
5 Esponenziali
6 Sinusoidali inverse
7 Logaritmiche
8 Funzioni composte
Queste funzioni le consideriamo reali a variabile reale, nel senso che sia x che la corrispondente y devono risultare reali. Ad es.
![]()
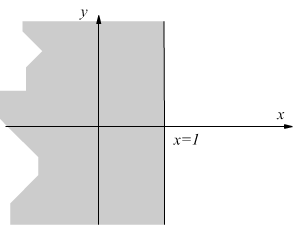
è una funzione reale per ogni x≥1 ma y non è una funzione reale di x per x<1; questo ci dice già che il grafico della y si troverà collocato soltanto nel semipiano delle x≥1 .
L'insieme dei valori che si possono attribuire alla x in modo da rendere la y reale è il campo di esistenza della funzione.
Campo di esistenza di funzioni razionali intere
I) ![]()
Il campo di esistenza coincide con l'insieme dei numeri reali. Le operazioni
da eseguire sul valore assegnato alla x sono sempre possibili, qualsiasi
sia questo valore. ![]()
II) ![]()
In questo caso il campo di esistenza è costituito da tutti i numeri reali,
infatti, le operazioni da eseguire sul valore assegnato ad x, sono sempre
possibili, qualunque sia questo valore.

i grafici risultanti sono dati dalle tre funzioni y1,y2
e y3.
Campo di esistenza di funzioni razionali fratte
Bisogna ovviamente ricordarsi che una espressione del tipo 3/0 è priva di
senso. Nel caso delle funzioni razionali fratte bisogna escludere tutti
i valori delle x che annullano il denominatore.
I) 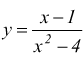
deve essere ![]() il
campo di esistenza è
il
campo di esistenza è ![]() .
.
II) 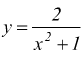
ma ![]() per
cui
per
cui ![]()
III) 
dato che: ![]() deve
essere
deve
essere
![]()
IV) 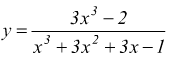 deve risultare
deve risultare ![]() ma
ma
![]() quindi
quindi ![]() .
.
V) 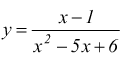 deve essere
deve essere ![]() il
trinomio di secondo grado è:
il
trinomio di secondo grado è:

deve risultare ![]() .
.
Campo di esistenza di funzioni irrazionali
Si tratta di considerare funzioni del tipo ![]() .
In questo caso dipende:
.
In questo caso dipende:
Se n é dispari, il radicando può assumere
qualunque valore.
Se n è pari, il radicando può assumere
solo valori positivi (o essere nullo).
Quindi avremo ![]() se
n è dispari, oppure
se
n è dispari, oppure ![]() se
n è pari.
se
n è pari.
I) 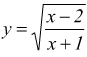 n
pari; deve essere
n
pari; deve essere 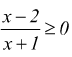



si riconosce come debba essere ![]() ma
attenzione al denominatore
ma
attenzione al denominatore ![]() dobbiamo
togliere il -1 dalla soluzione trovata.
dobbiamo
togliere il -1 dalla soluzione trovata. ![]()
II) ![]() deve essere
deve essere ![]()

risulta: 

III) ![]()
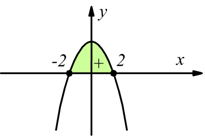
il radicando è una parabola con la concavità rivolta verso l'alto; questa parabola
è positiva (o nulla) per ![]()
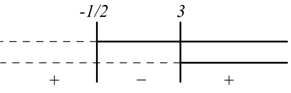
IV) 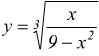
l'indice del radicale è dispari, il radicando può essere sia positivo
che negativo, in questo caso è sufficiente solo che ![]()

V) ![]()
deve essere ![]() ma
essendoci il modulo risulta essere
ma
essendoci il modulo risulta essere ![]() sempre; per cui
sempre; per cui ![]()
Quando invece si vuole rappresentare la funzione, la presenza del modulo, comporta lo studio dei seguenti casi:
a) ![]() cioè
cioè
![]() si ha
si ha ![]()
La funzione diventa ![]() il
cui campo di esistenza è
il
cui campo di esistenza è ![]()
b) ![]() cioè
cioè
![]() , si ha
, si ha ![]() e la funzione diventa:
e la funzione diventa: ![]() il cui campo di esistenza è
il cui campo di esistenza è ![]()
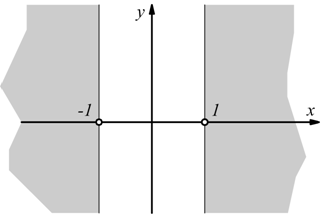
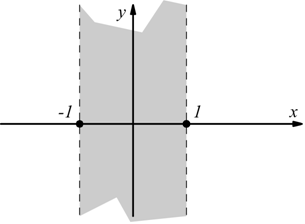
VI) 
deve essere 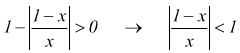
osservando che |x|=1 è verificata per x=±1 la disequazione |x|<1 è verificata
per -1< x <1 infatti si può separare in
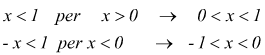
in conclusione -1< x <1 di conseguenza il nostro problema diventa:
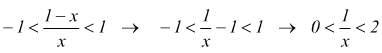
diventano due disequazioni:
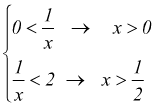


verificata certamente per x>1/2 e per la funzione si ha 
Quando invece si vuole rappresentare la funzione, la presenza del modulo, implica lo studio dei seguenti casi
a)  cioè
cioè
![]() si ha
si ha  e
la funzione diventa:
e
la funzione diventa:
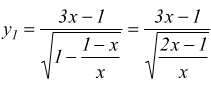
il cui campo di esistenza è dato dal sistema:
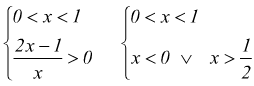
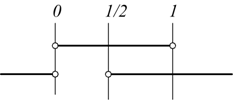
verificato per  quindi
quindi

b) 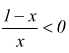 cioè
cioè ![]() risulta
risulta  e la funzione diventa:
e la funzione diventa:

il cui campo di esistenza viene ottenuto dal sistema:

![]()
Funzioni periodiche
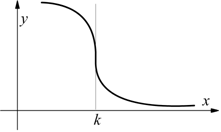
Supponiamo una y=f(x) definita su tutto l'asse reale, caratterizzata dal diagramma:
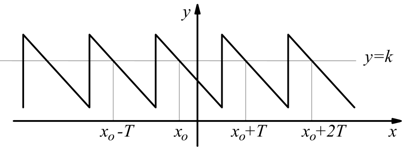
Osserviamo come la retta k interseca la curva di funzione nei punti indicati
xo-T, xo,xo+T, xo+2T.
Dal grafico si deduce che
f(xo-T)=f(xo)=f(xo+T)=f(xo+2T)=…=k
Dato che xo si può scegliere arbitrariamente, si può scrivere
in generale:
![]()
Le funzioni con questa peculiarità si dicono periodiche di periodo T. Se
si vuole verificare se una funzione è periodica basta controllare se esiste
un numero reale T tale che :
![]()
L'eventuale periodicità di una funzione implica che, stabilito il periodo
T, esse può essere studiata in un intervallo di ampiezza T qualsiasi.
cioè priva di significato, perchè qualsiasi numero moltiplicato per zero
restituisce come prodotto zero.
Funzioni sinusidali
Le funzioni periodiche più importanti sono quelle trigonometriche y=sinx e y=cosx il cui C.E. è (+∞ ,-∞ ) per le altre funzioni sinusoidali bisogna escludere dal C.E. i valori di x che le rendono indeterminate.Ad esempio per :
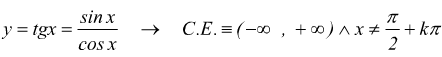
Una volta stabilito il CE, è conveniente determinare il periodo in modo da limitare lo studio della curva sul periodo T (più piccolo possibile).
Se prendiamo y=sinx, per quanto detto (applicando le regole di addizione) vale la
![]()
affinché sia verificata deve essere

il valore più piccolo è ![]() .
Per lo studio, si può considerare l'intervallo compreso fra 0 e 2π. Allo
stesso risultato si perviene studiando la y=cosx.
.
Per lo studio, si può considerare l'intervallo compreso fra 0 e 2π. Allo
stesso risultato si perviene studiando la y=cosx.
Se cerchiamo il periodo della y=tgx avremo:
![]()
applicando le formule di addizione :
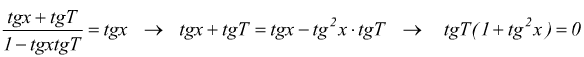
verificata per tgT=0 cioè per T=kπ (k=±1, ±2,..) il più piccolo valore che può assumere k è 1 quindi il periodo T della funzione è T=π ed il suo studio può essere limitato all'intervallo -π/2 fino a π/2.
Capita spesso dover studiare funzioni trigonometriche dove appaiono più funzioni elementari. Osserviamo le tre funzioni.

La prima (si è visto) ha periodo T=2π mentre si nota come la y=cos3x ha periodo T=2π/3 mentre la y=cos(x/2) ha periodo T=4π. Quindi, se si moltiplica per una costante k l'argomento di una funzione trigonometrica, il periodo risulta diviso per k.
Un'altra eventualità che può verificarsi è la presenza di un modulo.

Nelle funzioni elementari del tipo y=sinx y=cosx y=secx ed y=cosecx la presenza del modulo ha l'effetto di dimezzare il periodo.
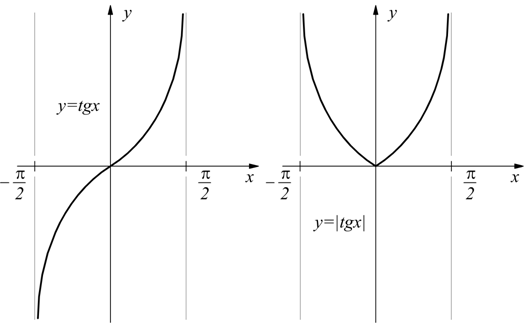
Si nota, invece che nelle funzioni del tipo y=tgx e y=ctgx l'introduzione del modulo non altera il periodo.
Esiste la possibilità che una funzione elementare del tipo y=sinx possa apparire come base di un elevamento a potenza.
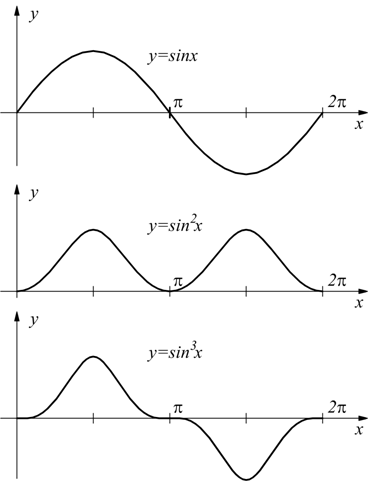
osservando l'andamento delle funzioni illustrate si conclude che quando si effettua un operazione di elevamento a potenza su una funzione elementare di periodo T, se l'esponente è pari, il periodo diventa T/2; se l'esponente è dispari il periodo rimane invariato T; mentre le funzioni y=tgx e y=ctgx non cambiano, in ogni caso il periodo, nel caso di un qualsiasi elevamento a potenza (pari o dispari).
Un elevamento a potenza può implicare che l'esponente sia un numero razionale, in tal caso si può parlare di radice n-esima di una funzione trigonometrica.
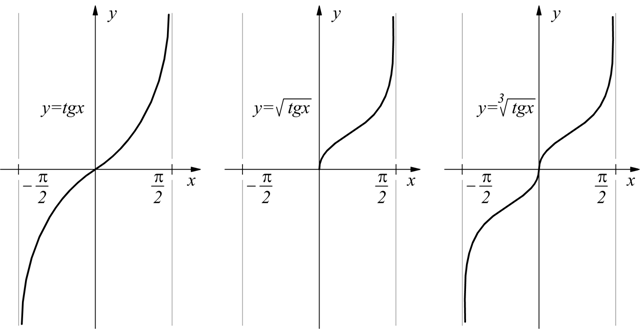
Come si nota per la funzione y=tgx, l'estrazione di radice non fa mutare il periodo.
Un caso particolare è rappresentato dalle operazioni di somma e differenza fra funzioni trigonometriche. Prendiamo in considerazione:


La funzione risultante avrà periodo T=4π. cioè il minimo comune multiplo dei periodi dei due addendi y=sin2x ed y=sin(x/2). Infatti è T1= e T2=4π mcm(π,4π)=4π.
Ad esempio se avessimo avuto T1=3π/8 e T2=9π/10 bisognava prima di tutto ricondurre i due periodi allo stesso denominatore: T1=15π/40 e T2=36π/40; poi bisognava notare l'mcm fra i due numeratori 15 e 36; mcm(15,36)=180. Il periodo risultante, sarebbe stato dunque:

Nel caso di prodotto o rapporto di due funzioni trigonometriche si ha che se le due funzioni hanno lo stesso periodo T, la funzione risultante avrà periodo T/2, come nel caso della
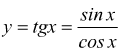
Se le due funzioni hanno periodo diverso la funzione risultante avrà il periodo pari all'mcm dei periodi delle due funzioni (come nel caso della somma/differenza).
|
Funzione |
Periodo |
Funzione |
Periodo |
 |
|||
 |
|||
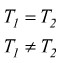 |
 |
||
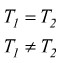 |
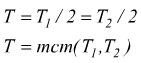 |
||
 |
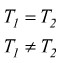 |
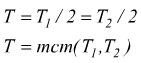 |
(°) funzioni elementari sinx, cosx, secx,cosecx.
(°°) funzioni tgx, ctgx.
Campo di esistenza per funzioni sinusoidali
I) 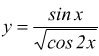
La cos2x ha periodo π e l'estrazione di radice non lo modifica; sinx ha periodo 2π il periodo T=mcm(π,2π)=2π. Limitiamo lo studio della funzione all'intervallo (0,2π). Affinché la funzione sia definita deve essere:
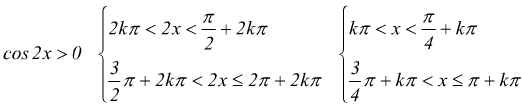
limitando le relazioni nell'intervallo (0,2π) avremo:

![]()
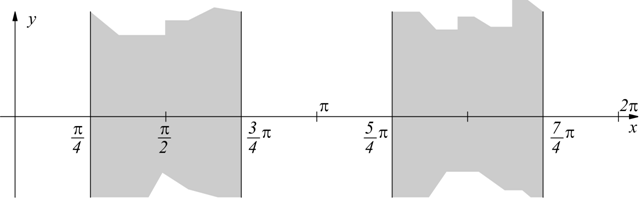
II) 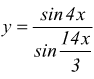
sin4x ha periodo T1=π/2. sin14x/3 ha periodo T2=3/7π. T=mcm(T1,T2)=3π. La funzione deve essere studiata nell'intervallo (0,3π). Per la sua definizione deve essere:
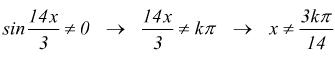
I punti di non definizione sono:

Funzioni esponenziali
Sono funzioni del tipo:
![]()
Da notare come debba essere a>0 (una potenza ad esponente reale è definita nel campo dei numeri reali solo se la base è positiva).
Infatti se a=-2 e x=1/2 si ha ![]() che
non è nel campo reale.
che
non è nel campo reale.

Attenzione! Nel caso a=1 si ha y=1 (retta parallela all'asse delle ascisse) per ogni valore di x.
Per a>0 la funzione è sempre positiva.
in tali condizioni ![]()
Campo di esistenza di funzioni esponenziali
I) 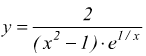
Perché la funzione sia definita deve essere ![]() quindi
quindi

Abbiamo ![]()
II) ![]()
deve essere:
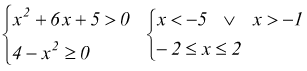
![]()
Funzioni sinusoidali inverse
Bisogna premettere un paio di cose sulla nozione di invertibilità di una funzione: data una y=f(x) è sempre possibile la sua inversa x=φ(y) se le due funzioni sono univoche, cioè se ad un valore di x corrisponde un solo valore di y e viceversa. Ad esempio in figura, le funzioni A e C sono invertibili, le funzioni B e D non sono invertibili.
Comunque, anche queste ultime, con appropriate restrizioni sono riconducibili a funzioni invertibili.
Comunque, anche queste ultime, con appropriate restrizioni sono riconducibili a funzioni invertibili. La B può essere invertita nell'intervallo x≥ 0 dove y è sempre crescente, oppure nell'intervallo x≤ 0 dove y è sempre decrescente. La funzione D y=sinx può essere invertita nell'intervallo [-π/2, π/2] dove è sempre crescente. Con l'inversione, il codominio della funzione originaria, diventa il dominio della funzione invertita.

Nel caso particolare della y=sinx avremo

In questo caso, il dominio di esistenza della y=sinx D=(-∞,+ ∞)
il suo codominio C=[-1,+1]. La funzione non è invertibile nel suo CE, ma
nel tratto (ad es.) [-π/2, π/2] lo è (y sempre crescente).
Può essere così definita la funzione
x=arcsin(y) con -1≤y≤1 e con -π/2≤x≤π/2
La rappresentazione più usuale di tale funzione prevede comunque che la variabile indipendente sia la x. per cui avremo

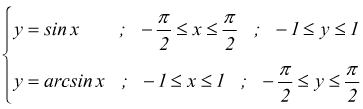

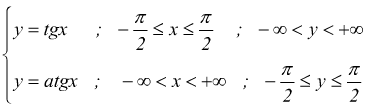







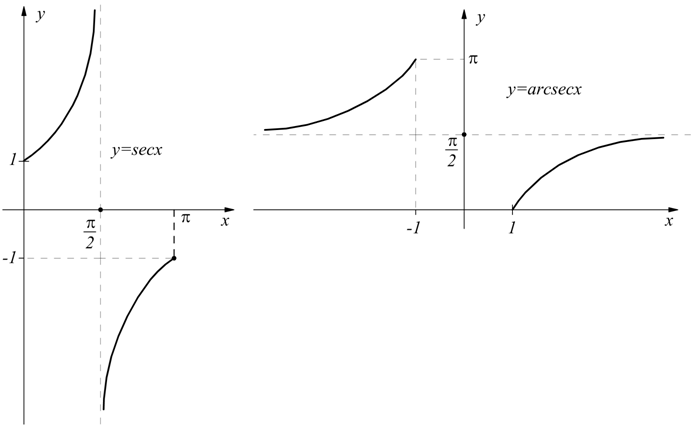

Campo di esistenza di funzioni sinusoidali inverse
I) ![]()
perché la funzione sia definita deve essere
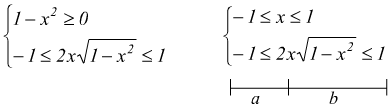
Per risolvere la seconda disequazione bisogna considerare i due casi x>0 e x<0. Per x<0 la (b) è sempre verificata; la (a) diventa:
sempre verificata.
Per x>0 la (a) è sempre verificata mentre la (b) diventa (possiamo elevare
a quadrato, dato che entrambi i membri sono positivi):
![]()
si può dire che la ![]() è
verificata per ogni valore di x.
è
verificata per ogni valore di x.
l'intero sistema è verificato per -1≤x≤1. Questo è il campo di esistenza.
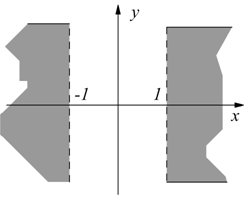
II)  per
le caratteristiche della funzione arcoseno deve essere:
per
le caratteristiche della funzione arcoseno deve essere:

1) per 4-ex>0 cioè per x < ln4 si ha
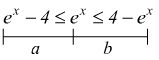
la prima parte a) ![]() è
sempre vera, basta quindi risolvere la b)
è
sempre vera, basta quindi risolvere la b)
![]()
questo caso viene quindi risolto dal sistema
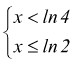

Verificata sicuramente per x≤ ln2
2) per 4-ex < 0 cioè per x > ln4 si elimina il denominatore cambiando i segni della disequazione.

la a) non è mai vera quindi questo sistema non ha soluzione.
Il campo di esistenza della funzione vale quindi ![]()

III)  per
le caratteristiche dell'arcoseno
per
le caratteristiche dell'arcoseno
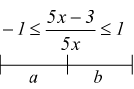 equivalente
al sistema
equivalente
al sistema
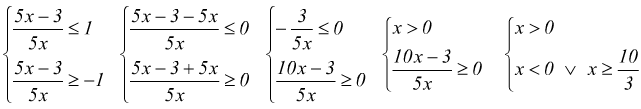


IV) 
Dato che |x|≥0 sempre, la realtà del radicale è assicurata, rimane da verificare la:

la b) è sempre vera, si risolve la a):
![]()
sempre vera:non vi sono restrizioni per il campo di esistenza ![]() .
.
Funzioni logaritmiche
Sono originate da equazioni algebriche del tipo:
![]() con
a > 0, a≠1 e b > 0;
con
a > 0, a≠1 e b > 0;
se sono rispettate queste condizioni è ammessa una ed una sola soluzione razionale o irrazionale; ad es.
2x=16 ha soluzione x=4 (razionale)
2x=7 ha una soluzione che è un numero irrazionale.
sotto queste condizioni ![]() .
Allora la funzione
.
Allora la funzione
![]() con con a > 0, a≠1 e y > 0 ha un campo di esistenza (-∞,+
∞) e ha per funzione inversa la
con con a > 0, a≠1 e y > 0 ha un campo di esistenza (-∞,+
∞) e ha per funzione inversa la
![]() con
-∞ < x < +∞ ed 0 < y < +∞
operando uno scambio di variabili si ottiene:
con
-∞ < x < +∞ ed 0 < y < +∞
operando uno scambio di variabili si ottiene:
![]()
con C.E=D=(-∞,+ ∞) con un codominio C=(0,+ ∞) il suo grafico è il seguente.

Campo di esistenza di funzioni logaritmiche
I) 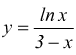
Per quanto detto deve essere l'argomento del logaritmo x > 0.
poi si dovrà avere ![]()
II) ![]()
per il logaritmo deve essere 2x+7 > 0 per la realtà del radicale deve essere 2x+1≥0.
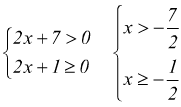
![]()
III) ![]()
per la realtà del logaritmo deve essere: sinx > 0 e questo si verifica
solo per ![]()
con k=0,±1, ±2, ±3.. dato che la funzione ha periodo 2π, si
può limitare lo studio solo nell'intervallo (0, π) come dire 0 < x <
π.
IV) 
la funzione ha periodo T=2π, si può limitarne lo studio in tale intervallo. Per la realtà del radicale deve essere:

dato che è cosx-2 < 0 sempre, deve essere:  studiando
il segno della frazione:
studiando
il segno della frazione:

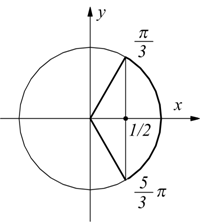

La nostra disequazione risulta soddisfatta per: 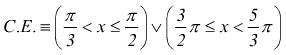
V)  dovrà
essere
dovrà
essere

l'ultima di queste diventa: 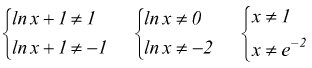
![]()
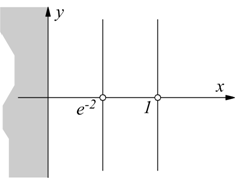
Intersezioni con gli assi
Gli assi cartesiani x ed y hanno rispettivamente equazione y=0 ed x=0. Per determinare le eventuali intersezioni con gli assi si pone: x=0 (se 0 appartiene al CE ) si trova il punto di intersezione con l'asse y (0,f(0)). y=0 risolvendo la f(x)=0 si trovano le intersezioni con l'asse x.
I) ![]()
Non ci sono intersezioni con l'asse y, dato che non si può porre x=0. Poniamo y=0.
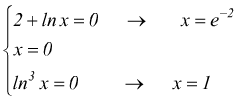
la seconda equazione non è accettabile dato
che x=0 non appartiene al CE.
II) ![]()
Per x=0 si ha y=-1, la curva interseca l'asse y nel punto P(0,-1).
Per y=0 il polinomio ![]() non
ammette soluzioni applicando la regola di Ruffini. Si può porre
non
ammette soluzioni applicando la regola di Ruffini. Si può porre ![]() rilevando
che deve esserci una intersezione fra la cubica al primo membro e la parabola
al secondo.
rilevando
che deve esserci una intersezione fra la cubica al primo membro e la parabola
al secondo.
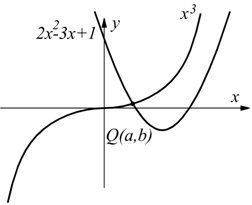
Questa intersezione è nel punto Q(a,b) a cui ci si può arrivare per approssimazione. La curva di funzione assegnata, interseca dunque l'asse delle ascisse x nel punto x=a.
Segno della funzione
Lo studio del segno della funzione è utile per sapere fin dall'inizio una idea anche approssimativa dell'andamento della stessa. Si tratta di sapere in quali intervalli la y è positiva oppure negativa.
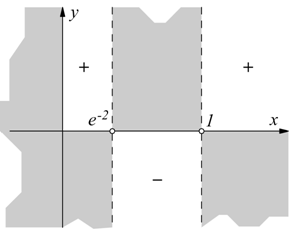
I) ![]()
La y è positiva ![]() per il segno del prodotto:
per il segno del prodotto:


da cui si desume che la funzione sarà localizzata nei settori indicati:
II) ![]()
Abbiamo già visto che il polinomio di terzo grado ammette una radice per x=a>0
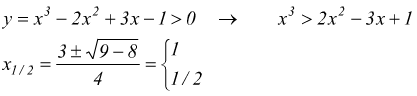

Dal grafico illustrato in precedenza si deduce
che y > 0 per x > a, con
0 < a < 1/2.
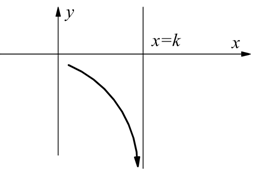
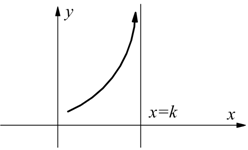
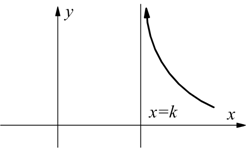
Condizioni agli estremi del campo di esistenza
La ricerca del campo di esistenza (CE) di una funzione serve per evidenziare
quali siano i valori della x per i quali la y non è definita.
Per sapere, puntualmente, quali siano i valori di y per dati valori di x,
basta sostituire al posto della x tali valori nella funzione; il valore
della y per i punti x che costituiscono gli estremi del CE non sono definiti,
ma possiamo studiare il comportamento della funzione all'approssimarsi di
questi estremi.

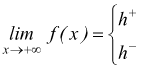

![]()
![]()
![]()
![]()

![]()


![]()
![]()
Discontinuità
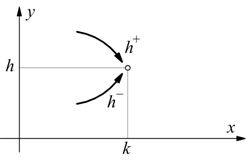
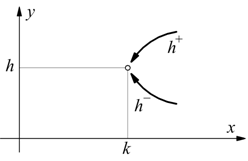
Se si considera una funzione y=f(x) su un punto di ascissa x=k, supponendo che sia:
![]()
con l finito. Se l=f(k) cioè se il limite è uguale al valore che la funzione
assume in k; la funzione si dice continua.
Se tale condizione non si verifica, la funzione è discontinua e k è un punto
singolare o di discontinuità della funzione.
Prendiamo ad es. la funzione:
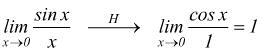
ma 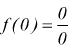 non
esiste. Per cui la funzione precedente è discontinua in x=0. La condizione
di discontinuità l≠ f(k) è qualificata in tre modi:
non
esiste. Per cui la funzione precedente è discontinua in x=0. La condizione
di discontinuità l≠ f(k) è qualificata in tre modi:
1) Discontinuità di Ia specie
Nel punto x=k esistono finiti i limiti destro e sinistro della funzione ma sono diversi.

![]()
2) Discontinuità di IIa specie
Nel punto x=k non esiste almeno uno dei due limiti destro o sinistro; oppure almeno uno di essi è infinito.
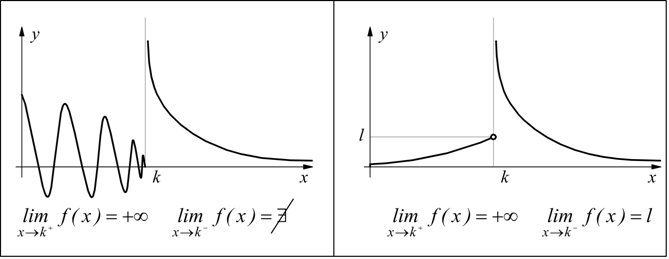
3) Discontinuità di IIIa specie
Nel punto di ascissa x=k esiste finito il limite della funzione ma non esiste f(k), oppure f(k) esiste ma è diverso dal limite.
Derivazione
La derivata consente di individuare molte caratteristiche della funzione.
Massimi, minimi, flessi.
E' opportuno ricordare che la derivata di una funzione in un punto della
curva, corrisponde geometricamente al valore del coefficiente angolare della
retta tangente alla curva di funzione che a sua volta corrisponde col valore
della tangente che tale retta forma con l'asse delle ascisse x, in quel
punto.

Considerando una funzione definita e continua nell'intervallo (a,b)

per a < x < p ⟶ f'(x) > 0 (funzione crescente)
per p < x < q ⟶ f'(x) < 0 (funzione decrescente)
per q < x < b ⟶ f'(x) > 0 (funzione crescente)
I punti P e Q sono punti di stazionarietà, essi si dicono punti di massimo e di minimo relativo (estremanti) e si individuano attraverso la seguente procedura:
1) si calcola la derivata y'.
2) si studia il segno della y'.
3) si verifica che la derivata si anulli nei punti in cui essa inverte
il suo segno.
Ad esempio: calcolare i punti di massimo e di minimo per la funzione:
![]()
1) calcolo della derivata ![]()
2) valutazione del segno della derivata:
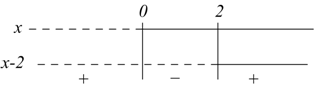
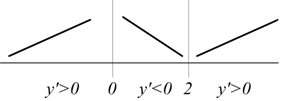
3) annullamento della derivata
dato che f'(0)=0 ed f'(2)=0 si deduce che in x=0 c'è un massimo e in x=2 c'è un minimo. Considerando il diagramma della y e della y' si ha:
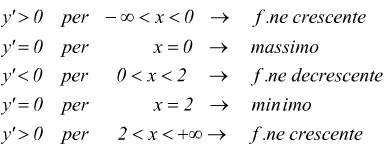
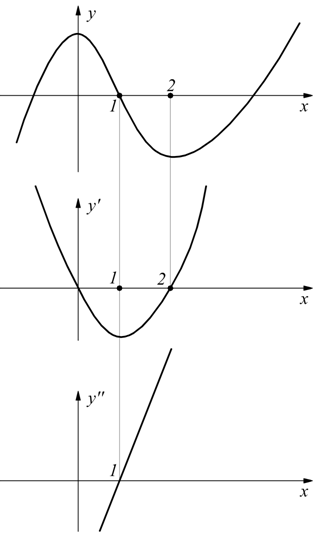
consideriamo poi la derivata seconda ![]() dai
diagrammi che abbiamo tracciato si conclude che:
dai
diagrammi che abbiamo tracciato si conclude che:
a) per i valori di x per i quali la y volge la concavità verso il basso
si ha y'' < 0.
b) per i valori di x per i quali la y volge la concavità verso il l'alto
si ha y'' > 0.
c) per i valori per i quali avviene il cambio di concavità y''=0.
Si possono trovare vari tipi di flessi:
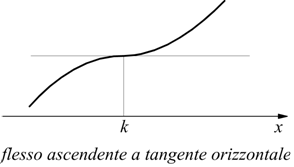
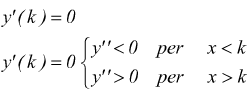

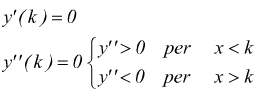

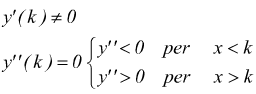


Punti angolosi cuspidi flessi a tangente verticale
Riassumendo: se la derivata prima è nulla si hanno massimi, minimi o flessi a tangente orizzontale. Se il flesso è a tangente obliqua, la derivata prima è diversa da zero ma si annulla la derivata seconda. Ma se la derivata prima è discontinua, cosa accade in quel punto? Osserviamo la funzione:
![]() si
ha:
si
ha:
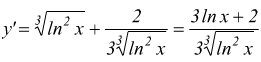
in x=1 la funzione è definita ed è y(1)=0, ma la y' non è definita in quel punto!
Sicuramente in x=1 non c'è ne massimo ne minimo e neanche un flesso a tangente orizzontale. Bisogna studiare li comportamento della y' nell'intorno di tale punto. Si ha:

Questa è una cuspide.
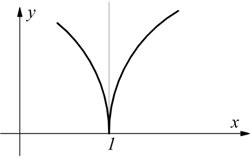
I vari casi che si possono presentare sono i seguenti:
cuspide verso il basso
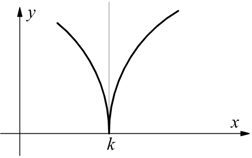
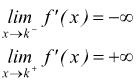
cuspide verso l'alto

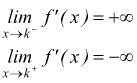
punto angoloso


punto angoloso
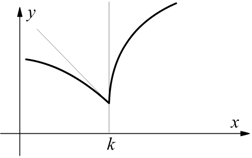
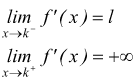
punto angoloso


punto angoloso


punto angoloso

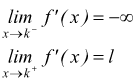
flesso verticale

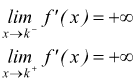
flesso verticale

Asintoti obliqui
Se una y=f(x) che da un certo valore di x in poi tende ad avvicinarsi ad una retta senza mai incontrarla, questa si dice asintoto della funzione.

Questo può verificarsi quando almeno uno degli estremi del CE è infinito. Come è possibile scoprire se una qualsiasi retta y=mx+q è un asintoto obliquo per la funzione studiata?
Tra tutte le rette possibili quella tangente alla curva di funzione all'infinito ha coefficiente angolare:
![]()
La quota q viene ottenuta tramite il concetto di asintoticità: il segmento
PQ può diventare piccolo quanto si vuole facendo tendere x all'infinito,
come dire:
![]()
Esprimendo analiticamente i due segmenti PT e QT:
![]() per cui:
per cui:
![]() o anche
o anche ![]()
Per individuare un asintoto obliquo si procede così:


se uno dei due limiti è infinito, non esiste asintoto obliquo. Se entrambi
sono finiti (m≠ 0) l'asintoto obliquo esiste.
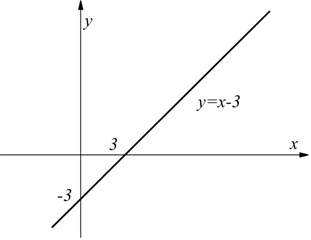
Esempio:
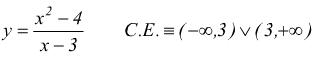


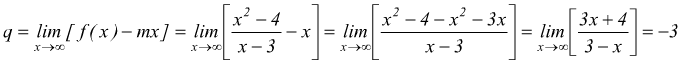
l'asintoto obliquo ha equazione y=x-3
 edutecnica
edutecnica