Equazioni con modulo (valore assoluto)

Le equazioni in valore assoluto sono quel tipo di equazione in cui l'incognita appare all'interno del simbolo di valore assoluto. Ad esempio:

Per risolvere questo tipo di equazione bisogna ricordare la definizione di valore assoluto di un numero reale, cioè:

∀x≡ per ogni valore di x

quindi per

Da questa definizione si deduce che:

Sempre dalla definizione si deduce che due numeri reali hanno lo stesso valore assoluto, se sono uguali oppure se sono opposti.

con ∨ ("oppure"). Valgono le poi le regole:

Il caso più semplice di equazione con modulo è dato dalla forma

con $A(x)$ e $B(x)$ espressioni algebriche nella variabile x. In tal caso si usa il seguente schema:

1 se $A(x)≥0$ l'espressione $|A(x)|=B(x)$ si riscrive come $A(x)=B(x)$;
2 se $A(x)<0$ l'espressione $|A(x)|=B(x)$ si riscrive come $-A(x)=B(x)$;

in sintesi l'insieme delle soluzioni dell'equazione $|A(x)|=B(x)$ è l'unione degli insiemi delle soluzioni dei due sistemi seguenti:

esempio: nell'equazione $|x+1|=3x$ il primo sistema è

e ammette soluzione $$x=1/2$$ perchè soddisfa la condizione $x≥0$. Il secondo sistema è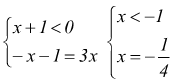

la soluzione $$x=-1/4$$ non può essere accettata perchè non soddisfa la condizione $x<0$.

Si conclude che l'unione delle soluzioni dei due sistemi S = S₁∪ S₂ è $$S=1/2$$.

Una casistica di equazioni con modulo, alcune delle quali con soluzione immediata è la seguente:

→ impossibile ; dato che il modulo di un numero reale non è mai negativo.

avremo:

infatti con il metodo tradizionale

Questo esempio mette in evidenza come le equazioni del tipo |A(x)|=k con k∈R possano essere risolte più velocemente delle altre perchè

1 se k<0 l'equazione |A(x)|=k è impossibile perchè il valore assoluto di un numero è sempre positivo o nullo.
2 se k=0 si ha solo A(x)=0 perchè il valore assoluto di un numero è 0 solo se il numero stesso è 0. Ad es.

3 se k>0 l'equazione |A(x)|=k equivale a A(x)=k ∨ A(x)= –k. Infatti per essere k>0 il numero deve essere uguale a k oppure al suo opposto –k

$|2x-3|=|4-3x|$ due numeri reali sono uguali in modulo, quando sono uguali oppure quando sono opposti:

$|x^2-6x+5|=5-x$ si risolve nel seguente modo:

l'insieme delle soluzioni è

$|4+x|=|5-2x|+7x$ prima si valuta per quali valori di x gli argomenti dei due moduli sono positivi:

si distinguono 3 casi:

Le soluzioni dell'equazione data, sono le soluzioni dei seguenti sistemi:

l'unica soluzione possibile è $$x=-1/4$$;

altri esempi di equazioni con valore assoluto sono riportati nei 30 esercizi risolti.

Interpretazione geometrica del valore assoluto

Il simbolo mi modulo può apparire anche all'interno di una funzione matematica, della quale si vuole ottenere la rappresentazione grafica. La più semplice funzione che può contenere in valore assoluto è la

per tracciare il grafico di questa funzione è sufficiente ricordare la definizione di valore assoluto che abbiamo esposto sopra.

quindi :
● se x ≥ 0 il grafico di y=|x| coincide con quello di y=x che è la bisettrice del primo quadrante;
● se x < 0 il grafico di y=|x| coincide con quello di y=–x che è la bisettrice del secondo quadrante; ottenendo il seguente grafico:

In generale, per tracciare i grafici di funzioni definite da equazioni che contengono qualche termine in valore assoluto occorre riscrivere queste equazioni informa equivalente in cui non compaiono più simboli di modulo come si è visto sopra visto che le funzioni con modulo sono funzioni definite per casi. Supponiamo di dover tracciare il grafico della funzione $y=x-|x-5|$ dalla definizione avremo

dunque

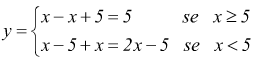
si tratta di comporre le due funzioni $y=5$ ed $y=2x-5$.

come si vede dal grafico la funzione coincide con il grafico della $y=5$ per $x≥5$ mentre coincide con il grafico della $y=2x-5$ per $x<5$.