Equazioni di secondo grado
Un'equazione è un'uguaglianza fra due espressioni contenenti un termine imprecisato che noi chiamiamo incognita, che implica la ricerca di determinati valori che chiamiamo soluzioni, i quali sostituiti al posto dell'incognita soddisfano l'uguaglianza cioè le rendono vera.
In un'equazione di primo grado si è visto come sia possibile trovare la soluzione che è unica. Ad es.
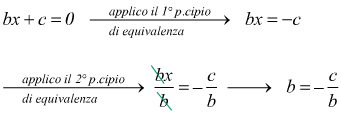
L'equazione di primo grado è caratterizzata dal fatto che in essa l'incognita x ha esponente 1.
Se invece si ha un'equazione che contiene l'incognita con esponente massimo 2, allora si dice che tale equazione è di secondo grado.
L'equazione di secondo grado, in forma normale o canonica è :
![]()
I coefficienti a b e c sono numeri reali; il terzo coefficiente c viene chiamato il termine noto.
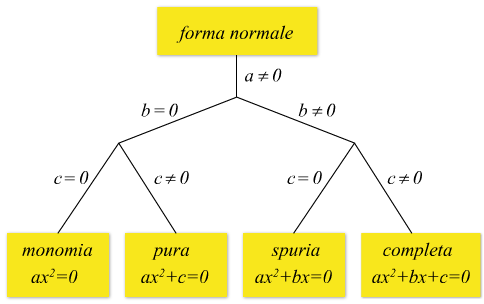
Un'equazione di secondo grado si dice completa quando sia a b che c sono diversi da zero; si dice incompleta quando il coefficiente b o il coefficiente c oppure entrambi sono uguali a zero.
Si hanno dunque i seguenti tipi di equazione:
• equazione di secondo grado pura se è riconducibile alla forma
![]() con
a≠0 e c≠0
con
a≠0 e c≠0
• equazione di secondo grado spuria se è riconducibile alla forma
![]() con
a≠0 e b≠0
con
a≠0 e b≠0
• equazione di secondo grado monomia se è riconducibile alla forma
![]() con
a≠0
con
a≠0
Equazione di secondo grado pura
Come già detto un'equazione di secondo grado pura si presenta nella forma
![]()
può essere risolta rispetto ad x2 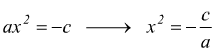 in
modo da ricondurla alla forma
in
modo da ricondurla alla forma
![]()
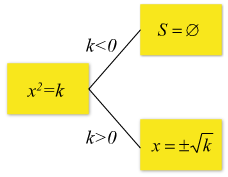
• se k>0 ci sono due numeri reali che possono avere come quadrato k. Cioè ci sono due soluzioni possibili
![]()
• se k<0 non ci sono soluzioni reali perchè nessun numero reale ha come quadrato un numero negativo.
Ad esempio : ![]() non
ha soluzioni: S=∅ dato che
non
ha soluzioni: S=∅ dato che ![]() non
si può risolvere; nessun numero elevato al quadrato fornisce un valore negativo.
non
si può risolvere; nessun numero elevato al quadrato fornisce un valore negativo.
Esistono, invece, casi dove si possono avere delle soluzioni; ad es.
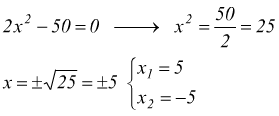
In questo caso l'insieme delle soluzioni è S={+5,-5}
Equazione di secondo grado spuria
Ogni equazione spuria, cioè del tipo
![]()
può essere risolta facendo il raccoglimento a fattor comune della x al primo membro
![]()
Per la legge di annullamento del prodotto, una delle soluzioni è certamente x=0 l'altra proviene imponendo che il binomio tra parentesi sia nullo
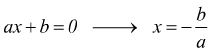 quindi
si ha sempre
quindi
si ha sempre

anche in questo caso si hanno due soluzioni, per esempio:
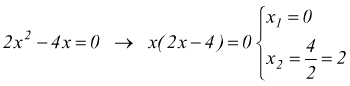
In questo caso l'insieme delle soluzioni è S={0,+2}
Equazione di secondo grado monomia
L'equazione di secondo grado monomia si riconosce perchè si presenta nella forma
![]()
con a≠0; è evidente che ammette l'unica soluzione x=0, tuttavia per
coerenza con i casi precedenti si afferma che si hanno due soluzioni coincidenti
per x=0.
Questo perchè essa può essere considerata un caso particolare dell'equazione
pura
![]() con
k=0
con
k=0
in tal caso le due soluzioni vengono a coincidere.
Equazione di secondo grado completa
L'equazione di secondo grado completa, anche chiamata trinomio di secondo grado, si presenta nella forma
![]()
con i tre coefficienti (a,b e c) diversi da zero. Il metodo standard per la sua soluzione porta a quella che viene chiamata la formula risolutiva dell'equazione di secondo grado
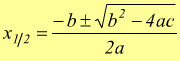
essa viene ottenuta applicando il metodo del completamento del quadrato, che consiste nell'effettuare delle manipolazioni algebriche in modo da trasformare il trinomio di secondo grado ax2+bx+c nella somma del quadrato di un binomio e di una costante. Si tratta di trasformare
![]()
se riusciamo a fare questa trasformazione, possiamo ricondurre l'equazione completa a quella di secondo grado pura; ammettendo k<0:
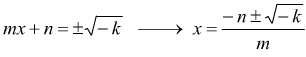
La chiave di volta è riuscire a trovare un numero che aggiunto al binomio ax2+bx produca un trinomio che corrisponda al quadrato di un binomio.
La soluzione arriva quando si osserva notando che quando a=1 per completare
il binomio in modo da ottenere un trinomio che sia un quadrato, bisogna
aggiungere il quadrato della metà di b cioè ![]() facciamo
un paio di esempi
facciamo
un paio di esempi
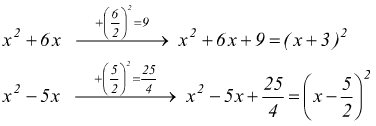
facciamo un esempio con un'equazione abbastanza semplice
![]()
al primo membro aggiungiamo e togliamo 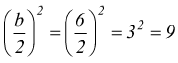
![]()
in questo modo non abbiamo fatto niente perchè +9-9=0 quindi l'operazione è lecita.

L'insieme delle soluzioni di questa equazione è S={+5;+1}
Per la dimostrazione bisogna ammettere a=1 quindi si ha
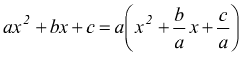
la metà di ![]() è
è
![]() ed
il suo quadrato è
ed
il suo quadrato è ![]() aggiungiamo
e togliamo questa quantità.
aggiungiamo
e togliamo questa quantità.
 dunque
dunque
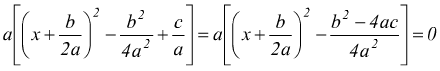
dato che a≠0 deve essere 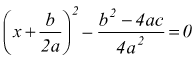 cioè
cioè
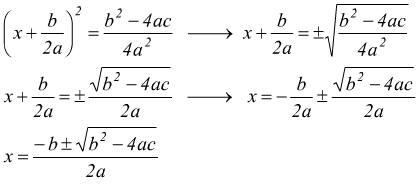
questa è la formula risolutiva dell'equazione di secondo grado. Applichiamola all'equazione precedente evidenziando i coefficienti
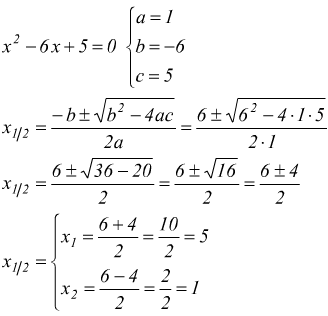
molto facile, dunque.
Discriminante
Il termine Δ=b2-4ac è chiamato discriminante dell'equazione di secondo grado, il suo valore è fondamentale nella discussione della stessa. Riprendendo una delle uguaglianze precedenti
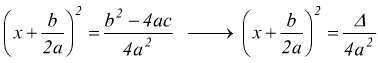
• Δ>0 al secondo membro abbiamo un numero reale positivo
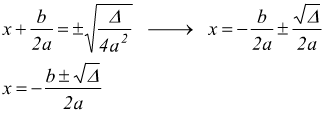
e l'equazione ha due soluzioni distinte
• Δ=0 l'equazione diventa
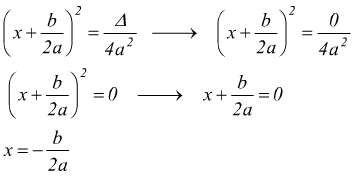
Per ragioni analoghe a quelle viste nel caso delle equazioni monomie si
dice che l'equazione ha due soluzioni coincidenti o che si ha una soluzione
doppia per 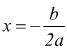
• Δ<0 l'equazione
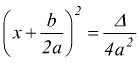 non
ha soluzioni
non
ha soluzioni
infatti per ogni x appartenente all'insieme dei numeri reali (∀x∈R) il primo membro può essere solo positivo o nullo (perchè elevato al quadrato) quindi non può essere uguale al secondo membro che sarebbe negativo. In sintesi
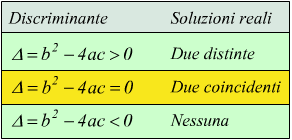
A questo punto, è evidente che per risolvere una qualsiasi equazione di
secondo grado completa ax2+bx+c=0 bisogna prima di tutto calcolare
il discriminante Δ in modo da cantrollare se ci sono soluzioni reali.
Se Δ≥0 si calcolano le soluzioni con la formula:
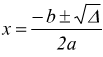
a : b : c :
Formula ridotta
Se dividiamo per due l'equazione completa

possiamo per comodità eseguire la sostituzione ![]() in
modo da ottenere
in
modo da ottenere
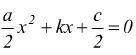 se
applichiamo la formula risolutiva dell'equazione di secondo grado si ha
se
applichiamo la formula risolutiva dell'equazione di secondo grado si ha
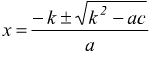 formula
ridotta
formula
ridotta
che è una formula risolutiva alternativa a quella ordinaria chiamata formula ridotta.
Relazione tra i coefficienti e le radici
Consideriamo il trinomio di secondo grado
![]()
supponiamo che abbia radici reali, cioè che sia Δ≥0, le due soluzioni x1 ed x2 sono date dalle formule
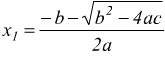 e
e 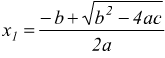
calcoliamo la somma di queste soluzioni
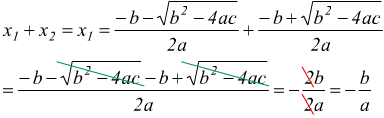
calcoliamo il prodotto di queste soluzioni
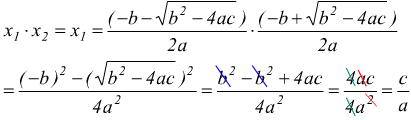
Le relazioni che intercorrono tra le soluzioni di un'equazione di secondo grado ed i coefficienti del suo trinomio rappresentativo sono:
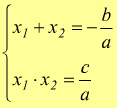
Scomposizione del trinomio di secondo grado
Il trinomio di secondo grado può sempre essere scritto come
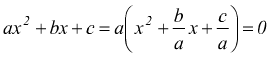 ma
ma
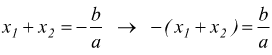 e
e 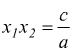 dunque
dunque
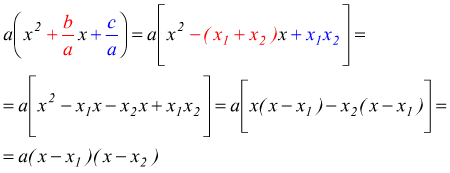
abbiamo dimostrato che se il trinomio ax2+bx+c ha radici reali cioè Δ≥0 esso può essere scomposto nella forma
![]()
con x1 e x2 soluzioni del trinomio assegnato.
 edutecnica
edutecnica