Disequazioni irrazionali
Una disequazione si dice irrazionale, quando in essa l’incognita appare sotto il segno di radice.
Per la sua soluzione, si cerca, ovviamente, fin da subito, di portarla in
forma razionale.
Per consuetudine si applica il principio di elevamento a potenza di entrambi
i membri della disequazione.
e 
se n è dispari si trasformano immediatamente in
e 
Ad esempio:
verificata per x < 3 o per x > 5.
Consideriamo ora, l'indice della radice n pari con il verso della disuguaglianza minore di <:
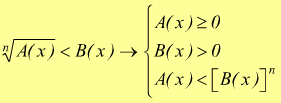
Per essere verificata deve risultare il radicando A(x)≥0 (condizione di esistenza del radicale) conseguentemente deve essere verificata la B(x)>0 ed infine si dovrà avere: A(x)<[B(x)]n ; in pratica la soluzione della disequazione coincide con la soluzione del sistema indicato.
Ad esempio: 
risulta
equivalente al sistema:
cioè 
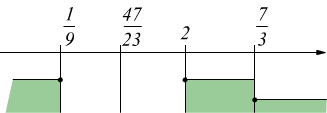
la rappresentazione grafica di questo sistema è:
Il sistema e quindi la disequazione è verificata per 
.
Consideriamo ora, sempre l'indice della radice n pari ma con il verso della disuguaglianza maggiore di >:
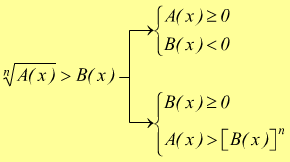
In questo caso è possibile che la relazione sia verificata sia quando A(x)≥0
e B(x)<0 oppure quando B(x)≥0 ed A(x)>[B(x)]n.
Le soluzioni della disequazione, sono, in questo
caso, tanto quelle dell'uno quanto quelle dell'altro, dei seguenti due sistemi
indicati.
Se chiamiamo S1 l'insieme delle soluzioni del primo sistema ed S2 l'insieme delle soluzioni del secondo sistema, la soluzione della disequazione sarebbe data da S ≡ S1 ∪ S2.
Nel caso in cui sia S1 =∅ sarà S=∅ ∪
S2=S2 ;
nel caso fosse S2 =∅ sarà S=S1 ∪ ∅=S1
Ad esempio : 
avremo,
per quanto visto sopra:
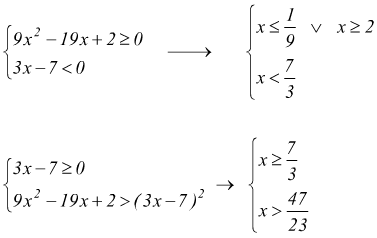
Il primo sistema è verificato per 
Il secondo sistema e verificato per 
la disequazione sarà verificata per l'unione dei due sistemi precedenti : 
.
