Disuguaglianze
Scritture come:
![]()
sono chiamate disuguaglianze numeriche e sono simboli matematici usati
per rappresentare relazioni tra quantità numeriche. In esse si notano i
simboli
< minore
> maggiore
≤ minore o uguale
≥ maggiore o uguale
Come si vede, simbolo (<) minore definisce un verso, mentre il simbolo
(>) maggiore definisce un verso opposto.
Nelle disuguaglianze (come si è detto nelle uguaglianze) si chiama primo
membro l'epressione che sta a sinistra del simbolo di disuguaglianza mentre
si chiama secondo membro l'espressione che si trova a destra del simbolo
di disuguaglianza.
Una disuguaglianza può essere vera o falsa:
3>2 è una disuguaglianza vera
3>4 è una disuguaglianza falsa
Le disuguaglianze false rappresentano un assurdo matematico e dunque non
possono essere accettate.
Anche le disuguaglianze (nel loro piccolo) hanno alcune proprietà:
1 Aggiungendo o sottraendo ad entrambi i membri di una disuguaglianza lo stesso numero il verso della disuguaglianza non cambia.
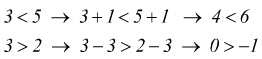
2 Moltiplicando o dividendo entrambi i membri di una disuguaglianza per lo stesso numero positivo il verso della disuguaglianza non cambia
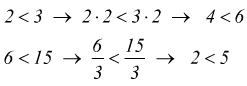
3 Moltiplicando o dividendo entrambi i membri di una disuguaglianza per lo stesso numero negativo, si ottiene una disuguaglianza di verso opposto.

Per cambiare il verso di una disuguaglianza sarà dunque sufficiente moltiplicare (o dividere) il primo ed il secondo membro per -1.
Disequazioni
Una disuguaglianza in cui appare un'incognita, viene chiamata disequazione
ad un'incognita.
Se in una disequazione si sostituisce un numero al posto di una incognita,
la disequazione si trasforma in una diseguaglianza che può essere vera o
falsa.
Un numero è soluzione di una disequazione se, sostituito all'incognita rende
vera la disequazione stessa.
Risolvere la disequazione significa trovare l'insieme delle soluzioni.
Questo insieme è in generale un intervallo o una unione di più intervalli.
Viene definito il dominio di una disequazione (D) come l'insieme dei numeri
reali che se sostituiti all'incognita trasformano la disequazione in una
disuguaglianza dotata di senso (o vera o falsa). Ad es.
![]() D
≡ R cioè, il dominio coincide
con l'insieme dei numeri reali, mentre
D
≡ R cioè, il dominio coincide
con l'insieme dei numeri reali, mentre
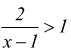 D
≡ R-[ 1 ] perchè il valore 1 annulla il denominatore rendendo l'espressione
al primo membro priva di senso.
D
≡ R-[ 1 ] perchè il valore 1 annulla il denominatore rendendo l'espressione
al primo membro priva di senso.
Due disequazioni sono equivalenti se hanno lo stesso insieme di soluzioni.
Il metodo risolutivo di una disequazione è lo stesso che si è visto nel
caso delle equazioni; cioè si tratta di trasformare la disequazione iniziale
progressivamente in altre disequazioni equivalenti più semplici, ottenute
manipolando la disequazione di partenza.
Tutti i passaggi devono rispettare i seguenti principi
di equivalenza che sono diretta conseguenza delle proprietà delle
disuguaglianze viste sopra.
1° principio di equivalenza per le disequazioni
: Se a entrambi i membri di una disequazione si aggiunge o si sottrae la
stessa quantità la disequazione non cambia.
2° principio di equivalenza per le disequazioni :
Moltiplicando o dividendo entrambi i membri di una disequazione per una
quantità positiva, la disequazione non cambia.
3° principio di equivalenza per le disequazioni :
Moltiplicando o dividendo entrambi i membri di una disequazione per una
quantità negativa e cambiando senso al simbolo di disuguaglianza, la disequazione
non cambia.
Disequazioni di primo grado
![]()
la soluzione della prima di queste sarà ad.es.
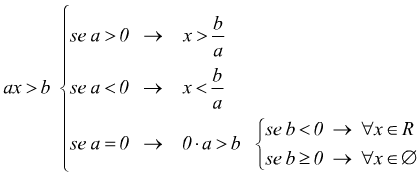
Esempio :
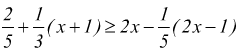 D ≡ R
D ≡ R
moltiplico per 5 a sinistra e a destra
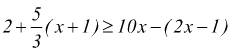 moltiplico
per 3 a sinistra e a destra
moltiplico
per 3 a sinistra e a destra
![]() svolgo
le parentesi
svolgo
le parentesi
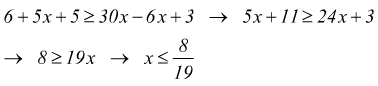
 edutecnica
edutecnica