Derivata di una funzione
Il concetto di derivata di una funzione ad una variabile, è uno dei più
importanti e fondamentali sia della matematica pura, sia di ogni sua applicazione
ed è quello su cui si basa l'intera costruzione del calcolo differenziale.
La creazione del calcolo infinitesimale, come metodo potente, sistematico
e compiuto può essere riferito alla seconda metà del 1600 quando Newton
e Leibniz, indipendentemente l'uno dall'altro, introdussero la nozione di
derivata e di differenziale sviluppando le relative regole di calcolo.
Ma in matematica, come in tutte le discipline scientifiche, le idee non sorgono
improvvise; esse sono sempre il risultato di una preparazione più o meno
lunga.
Tracce e approcci a questo tipo di calcolo sono stati riscontrati nelle
opere di Archimede mentre i lavori di Cavalieri e Torricelli (allievi di
Galileo) sono da considerare precursori delle teorie di Newton e Leibniz
di cui hanno contribuito a preparare il terreno.
Ipotizziamo che la funzione y=f(x) è definita nell'intervallo chiuso [a,b]
fissiamo un punto x appartenente a questo intervallo; consideriamo un altro
punto x+h appartenente anch'esso ad [a.b]. La quantità h è l'incremento
subìto dalla x per passare al punto x+h. In concomitanza di questo
incremento, la funzione f(x) passa dal valore f(x) al valore f(x+h) quindi
la funzione subisce l'incremento:
![]()
viene così definito il rapporto incrementale
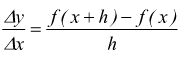
Se al tendere di h a zero il rapporto incrementale tende ad un limite finito,
questo si chiama derivata (prima) della funzione f(x).
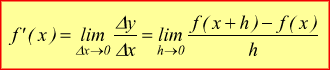
Se la derivata f'(x) esiste per ogni punto dell'intervallo [a,b] in cui è definita la f(x) quest'ultima si dice derivabile nell'intervallo specificato.
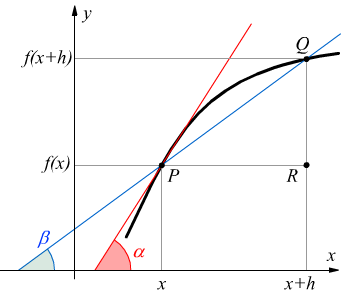
L'interpretazione geometrica è semplice: prendiamo un punto P appartenente al grafico della funzione, diciamo che x è la sua ascissa e f(x) la sua ordinata. Poi prendiamo un altro punto Q appartenente alla funzione, di ascissa x+h e di ordinata f(x+h). Consideriamo la retta PQ (quella blu) .
Quando Q percorre la curva avvicinandosi a P, la retta PQ assume una posizione limite che possiamo ritenere tangente alla curva di funzione in P.
Dal triangolo PQR si ha:
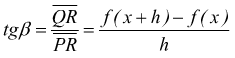
Quando h tende a zero, Q tende a P e la secante tende alla tangente in
P (linea rossa).
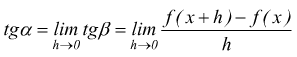
Ricordiamo che le tangenti tgα e tgβ sono i coefficienti angolari
delle rette associate. Se ne ricava:
![]()
Significato geometrico di derivata
Dall'ultima formula che abbiamo calcolato si può comprendere quella che può essere considerata l'interpretazione geometrica della derivata di una funzione:
il coefficiente angolare della retta tangente ad una linea di equazione $y=f(x)$ in un suo punto, è uguale alla derivata di $f(x)$ in quel punto.
Possiamo allora scrivere l'equazione della retta tangente alla linea di equazione $y=f(x)$ nel punto di ascissa $x_o$ ed ordinata $y_o=f(x_o)$ come
$y-f(x_o)=f'(x_o)⋅(x-x_o)$
prendiamo una funzione, ad esempio una bella parabola: $y=x^2-8x+15$ calcoliamo il rapporto incrementale
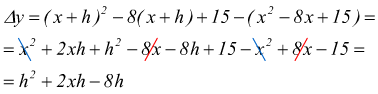
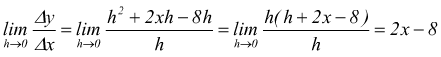
sappiamo che questa parabola ha la concavità rivolta verso l'alto ed interseca l'asse delle ascisse nei punti x=3 ed x=5 ; l'ascissa del vertice è collocato in xo=4. In tale punto avremo
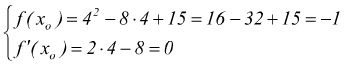
Notiamo come la derivata della funzione nel punto xo=4 sia nulla, è dunque nullo anche il coefficiente della retta tangente alla linea di funzione assegnata che significa che in quel punto la retta tangente alla curva della funzione è orizzontale! L'equazione della retta tangente alla y=f(x) nel punto xo=4 è infatti
![]()
cioè è una retta orizzontale passante per l'ordinata y=-1.

nello schema interattivo, viene riportato il valore numerico della derivata della funzione in corrispondenza del punto appartenente alla curva selezionato, in alto a destra, sono invece riportate le coordinate xy del punto selezionato.
Un altro esempio ci porterebbe a considerare un valore infinito per la
derivata, e questo significa che la retta tangente in quel punto alla curva
di funzione è verticale.
Calcoliamo la derivata della funzione $y=√^3{x}$ nel
punto xo=0
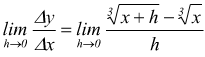 calcolata
per x=xo=0 fornisce
calcolata
per x=xo=0 fornisce 
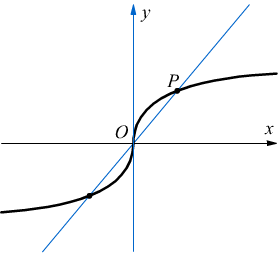
la derivata della funzione nel punto xo=0 è infinita e la tangente al grafico della funzione nel punto xo=0 è la retta verticale di equazione x=0.
Dal disegno che segue si vede come il coefficiente angolare della secante OP quando P tende ad O (sia da destra che da sinistra) restando sulla curva tende a +∞.
La nozione di derivata si presenta spontaneamente in tutte le discipline di applicazione della matematica. Ad esempio in fisica è molto importante la nozione di velocità intesa come derivata dello spazio rispetto alla variabile tempo. Supponiamo di conoscere la legge oraria con cui varia lo spazio percorso da un punto materiale in funzione del tempo: s=f(t) se consideriamo i due istanti successivi t e t+h il rapporto
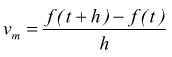
si chiama velocità media nell'intervallo di tempo h ed è funzione di h, ed il suo limite per h tendente a zero è la velocità corrispondente al termpo t, o come si dice solitamente è la velocità all'istante t. Dunque:
La velocità di un punto materiale in moto è uguale alla derivata dello spazio da esso percorso, rispetto al tempo.
![]()
In generale la nozione di velocità media e di velocità si estende a tutti i fenomeni fisici in cui la grandezza variabile y è funzione del tempo t.
Derivabilità e continuità
Se una funzione è derivabile in un punto x, questa è continua in quel punto. Infatti essendo
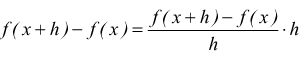 si
ha
si
ha

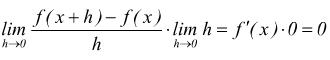 quindi
essendo
quindi
essendo
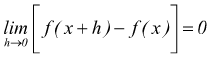 la
funzione f(x) è continua nel punto x.
la
funzione f(x) è continua nel punto x.
Il teorema inverso non sussiste. Infatti si conoscono funzioni che sono continue in ogni punto di un intervallo e non hanno derivata in nessun punto.
Derivate di funzioni elementari
Derivata di una funzione costante
Se y=k con k numero relativo qualsiasi, si ha y'=0. Infatti l'incremento
della funzione y per qualsiasi incremento h della variabile è nullo.
Si ha quindi

![]()
Derivata della funzione lineare
Data la funzione $y=mx+q$ definita $∀x ∈ R$, il rapporto incrementale,
se h ≠ 0 è
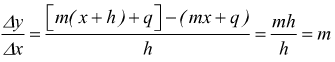
e si ottiene y'=m, si scrive ![]()
Derivata della funzione potenza ad esponente intero positivo
Se y=xn con n intero assoluto si ha:  e
qui dobbiamo ricorrere allo sviluppo della potenza n-esima del binomio.
e
qui dobbiamo ricorrere allo sviluppo della potenza n-esima del binomio.
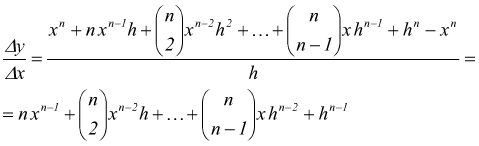
passando al limite per h→0, 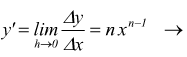
![]()
La potenza ad esponente intero assoluto ha per derivata il prodotto dell'esponente per la potenza ad esponente diminuito di 1. In particolare per n=1 si ha Dx=1.
Derivata della funzione seno
Data la funzione y=sinx definita ∀x ∈ R, il rapporto incrementale,
se h ≠ 0 è 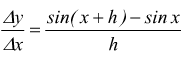
che sviluppato attraverso la formula di addizione del seno e poi con quella
di duplicazione del coseno diventa
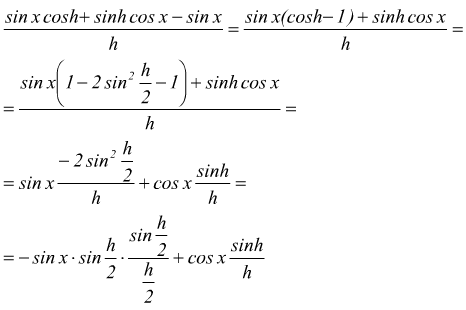
passando al limite per h→0
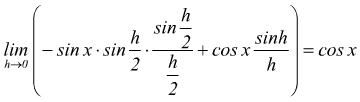
dunque y'=cosx e si scrive ![]()
Derivata della funzione coseno
Se procediamo come nel caso precedente è possibile dimostrare che se y=cosx
si ha y'=-sinx e scriveremo
![]()
Derivata della funzione logaritmica
Data la funzione logaritmica con y=logax con a > 0 ed a ≠
1 definita ∀x ∈ R+, il rapporto incrementale, se
h ≠ 0 è
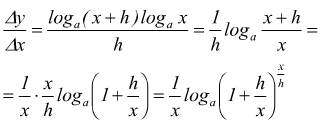
dopo aver posto $$t=x/h$$ e considerando che è sempre $x > 0$ si ha
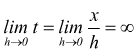 ne
consegue
ne
consegue
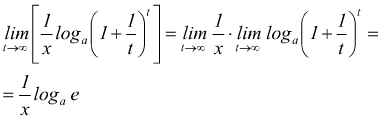
in definitiva $$y'=1/xlog_a{e}$$ si
ha concludendo 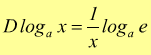
in particolare se $a=e$ numero di Nepero si ha $$y'=1/xln\,e=1/x$$ dunque
è 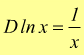
Derivata della funzione esponenziale
Data la funzione esponenziale $y=a^x$ con $a > 0$ definita per ogni
valore di x reale, il rapporto incrementale, se h ≠ 0 è
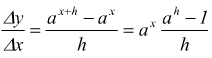
poi ponendo 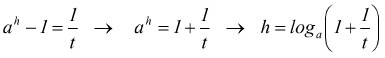
poiché 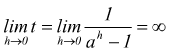 si ha
si ha
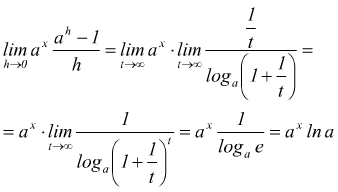
in definitiva si ha $y'=a^x\,ln\,a$ dunque
![]()
in particolare se a=e numero di Nepero si ha ![]()
Regole di derivazione
Considerando esclusivamente funzioni derivabili, possono essere espressi i seguenti teoremi.
1 Derivata del prodotto
di una funzione per una costante
Se è $y=k·f(x)$ con $k$ numero reale qualsiasi si ha
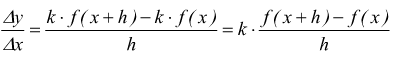
passando al limite per h→0 si ottiene
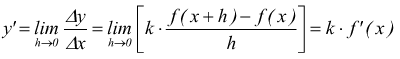
dunque ![]()
La derivata del prodotto di una funzione per una costante è uguale al prodotto della costante per la derivata della funzione, come mostrato dai seguenti esempi.
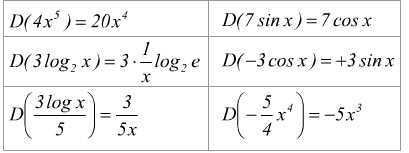
2 Derivata di una somma di
funzioni
Se è $y=f(x)+g(x)$ si ha
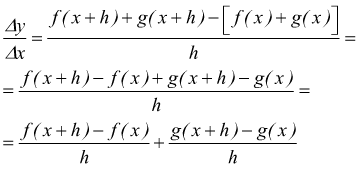
quindi passando al limite per h→0 si ottiene
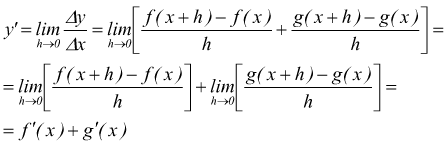
dunque: ![]()
Questo teorema si estende facilmente al caso di più funzioni, quindi: la
derivata della somma algebrica di più funzioni è uguale alla somma algebrica
delle loro derivate.
Esempi:
● ![]()
● 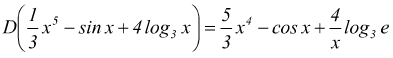
● 
3 Derivata del prodotto di
due funzioni
Se è $y=f(x)·g(x)$ si ha
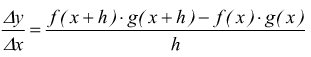
addizionando e sottraendo al numeratore f(x)·g(x+h)

raccogliendo a fattor comune g(x+h) nel primo e nel quarto addendo ed f(x) nel secondo e nel terzo

essendo f(x) e g(x) derivabili e quindi continue, è $\lim↙{h→0}\,{g(x+h)=g(x)$ di
conseguenza
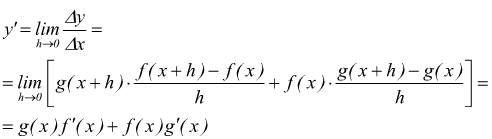
si conclude 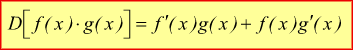
La derivata del prodotto di due funzioni è uguale alla somma dei prodotti di ciascuna di esse per la derivata dell'altra.Esempi:
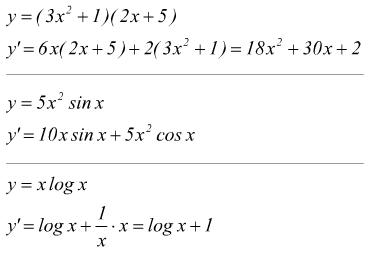
questo teorema può essere esteso al prodotto di più di due funzioni. Nel caso di tre funzioni $y=f(x)⋅g(x)⋅p(x)$ si ha
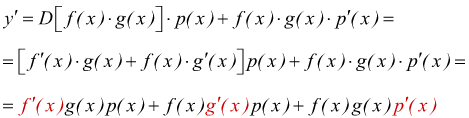
come ad esempio
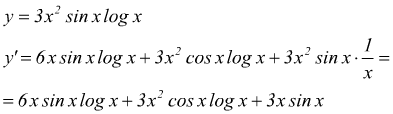
4 Derivata della funzione
reciproca
Se è $$y=1/{f(x)}$$
si ha

ora se passiamo al limite per h→0 dobbiamo notare che è$\lim↙{h→0}\,{f(x+h)=f(x)$ dunque
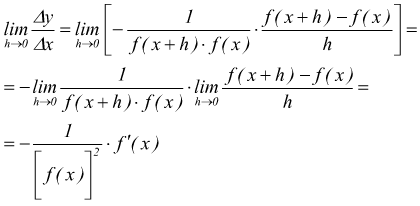
si conclude che 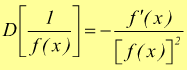
interessante il caso particolare $$y=1/x^n$$
si ottiene infatti $$y'=-{n⋅x^{n-1}}/{[x^n]^2}=-{nx^{n-1}}/{x^{2n}}$$
poi dividendo numeratore e denominatore per $x^{n-1}$, si ottiene:
$$y'=-n/x^{n+1}$$
5 Derivata del quoto di due
funzioni
Se è $$y={f(x)}/{g(x)}=f(x)⋅1/{g(x)}$$ allora
per il teorema del prodotto e della funzione reciproca si ha:
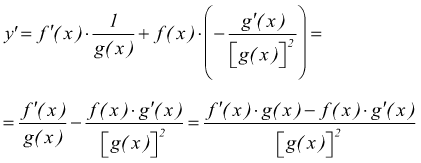
in definitiva 
La derivata del quoto di due funzioni è uguale ad una frazione che ha come denominatore il quadrato del denominatore e come numeratore la differenza tra la derivata del numeratore per il denominatore non derivato e la derivata del denominatore per il numeratore non derivato.
L'esempio che obbligatoriamente si fa per questo tipo di derivazione è
quello della tangente trigonometrica: $$y=tgx={sinx}/{cosx}$$
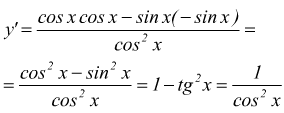
l'ultimo passaggio si ottiene ricordando che è sin2x+cos2x=1
6 Derivata di funzione composta
Dobbiamo prima definire una funzione composta, spesso chiamata funzione
di funzione.
Sia t=f(x) definita in un intervallo [a, b]. Se I è l'insieme dei valori
assunti da t quando x varia in [a, b] e sia y=F(t) una funzione di t definita
nell'insieme I.
Per ogni valore di x ∈ [a, b] resta allora definito un valore si y.
Si piò allora affermare che y è funzione di x per tramite di t e si scrive
y=F[f(x)].
Diremo che y è funzione di x oppure funzione composta di x mediante la t.
Ad esempio $y=ln(x^2+3)$ è una funzione composta di $x$ mediante $t=x^2+3$
con $y=ln(t)$ .
Dopo questa premessa, determiniamo la derivata della funzione y=F[f(x)]
funzione composta di x mediante f(x). Se è t=f(x) e si fa subire ad x l'incremento
h la f(x) subirà un incremento che indichiamo k. Quindi
![]() si
ha, allora
si
ha, allora 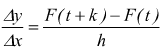 moltiplicando e dividendo per k
moltiplicando e dividendo per k
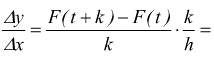
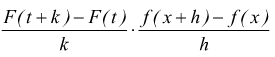
poiché f(x) è derivabile e quindi continua $\lim↙{h→0}[{f(x+h)-f(x)]=0$
cioè $\lim↙{h→0}k=0$ passando
al limite per h→0

si conclude che ![]()
La derivata di una funzione di funzione è uguale al prodotto della derivata
che si ottiene considerando come variabile la funzione da cui essa dipende
per la derivata di tale funzione. Esempi:
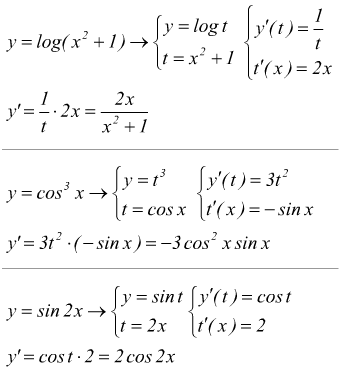
Questo teorema è, ovviamente, coerente con la formula di derivazione per la funzione $y=x^n$, infatti $y=x^n$ con n numero reale, può essere riscritta come $y=e^{n\,lnx}$ funzione composta
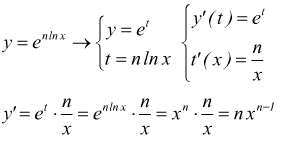
7 Derivata di $f(x)^{g(x)}$
Se è $y=f(x)^{g(x)}$ prendendo
il logaritmo neperiano di entrambi i membri
![]()
derivando entrambi i membri rispetto ad x
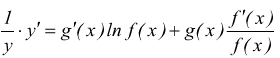 di
conseguenza
di
conseguenza
 dunque
dunque

8 Derivata della funzione
inversa
Se y=f(x) è una funzione invertibile nell'intervallo [a, b] ed è x=g(y)
la sua funzione inversa sarà
![]() derivando
entrambi i membri rispetto ad x, si ottiene
derivando
entrambi i membri rispetto ad x, si ottiene
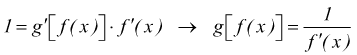 in
definitiva è:
in
definitiva è:
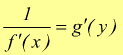 si
conclude che le funzioni inverse hanno derivate reciproche
si
conclude che le funzioni inverse hanno derivate reciproche
Usando quest'ultimo teorema è possibile calcolare la derivata della funzione arcoseno, funzione inversa del seno.
![]() ha
come funzione inversa
ha
come funzione inversa
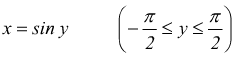 quindi
essendo $$y'=1/{x'}$$ avremo
quindi
essendo $$y'=1/{x'}$$ avremo
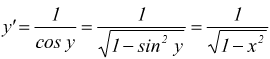 dunque
dunque
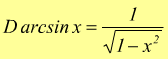
Un ragionamento analogo si può fare per la funzione arcocoseno.
![]() ha
come funzione inversa
ha
come funzione inversa
![]() essendo
$$y'=1/{x'}$$ avremo
essendo
$$y'=1/{x'}$$ avremo
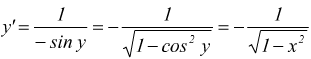 dunque
dunque
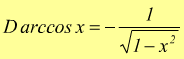
anche per la funzione arcotangente può essere usato lo stesso teorema.
$y=arctgx$ con x reale qualsiasi ha come funzione inversa
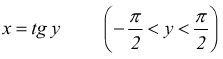 essendo $$y'=1/{x'}$$
si
ha:
essendo $$y'=1/{x'}$$
si
ha:
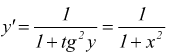 dunque
dunque
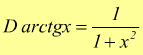
Teoremi sulle funzioni derivabili
Teorema:Una funzione derivabile, è crescente
nel punto xo se la derivata della funzione è positiva in xo.
E' decrescente in xo se la derivata è negativa in xo.
Definizione: una funzione f(x) ha nel punto xo appartenente al suo intervallo di definizione un massimo relativo, in xo, se esiste un intorno di xo, tale che la funzione sia crescente a sinistra e decrescente a destra di xo. Si ha un minimo relativo se esiste un intorno di xo, tale che in esso la funzione sia decrescente a sinistra e crescente a destra.
Teorema:Se la funzione f(x), derivabile ha un massimo o un minimo in xo; la sua derivata in xo è nulla.
Teorema di Rolle:Se una funzione è definita e derivabile in ogni punto dell'intervallo [a,b] e prende valori uguali negli estremi di esso, la sua derivata si annulla almeno in un punto dell'intervallo stesso.
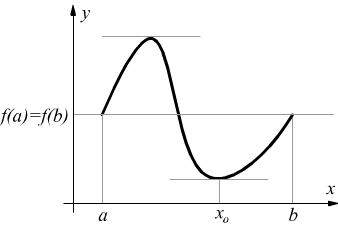
Teorema di Cauchy: se in un intervallo [a,b] le due funzioni f(x) e g(x) sono derivabili e la derivata di g(x) non è mai nulla, in tutto l'intervallo esiste un punto x0 per il quale risulta:
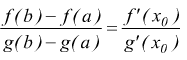
Teorema di Lagrange (del valor medio):Se una f(x) è derivabile in ogni punto di un intervallo ed a e b sono due punti dell'intervallo, esiste un punto xo compreso fra a e b per il quale si ha:
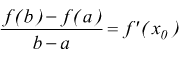
Infatti tracciato il diagramma della funzione y=f(x) se A e B sono i punti appartenenti alla funzione in corrispondenza delle ascisse a e b il rapporto:
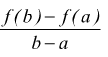
è il coefficiente angolare della retta AB.
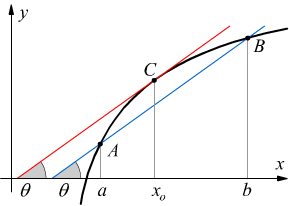
Se C è il punto di ascissa xo, ![]() è
il coefficiente angolare della tangente al grafico nel punto C. Il teorema
esprime l'esistenza di almeno un punto all'interno dell'arco AB della
curva, nel quale la tangente risulta parallela alla retta AB.
è
il coefficiente angolare della tangente al grafico nel punto C. Il teorema
esprime l'esistenza di almeno un punto all'interno dell'arco AB della
curva, nel quale la tangente risulta parallela alla retta AB.
Teorema di l'Hospital:se due funzioni continue f(x) e g(x) tendono a zero per x che tende ad a, il limite del loro rapporto è uguale al limite del rapporto delle loro derivate, se quest'ultimo esiste.Cioè se è:
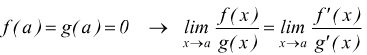
Differenziale di una funzione
Se $y=f(x)$ è derivabile si ha: $$\lim↙{Δx→0}\;{Δy}/{Δx}=f'(x)$$ con una scrittura fuori dal segno di limite, si ha
$${Δy}/{Δx}=f'(x)+ε$$ ovviamente con $ε$ piccolo a piacere e con la proprietà $\lim↙{Δx→0}\,ε=0$
moltiplicando entrambi i membri dell'equazione suddetta per $Δx$ si ha $Δy=Δx⋅f'(x)+Δx⋅ε$
$Δy$ e $Δx·f'(x)$ sono infinitesimi dello stesso ordine dato che il limite del loro rapporto è $ f'(x)$ finito. Mentre $Δx·ε$ è infinitesimo di ordine superiore rispetto a $Δx$ e quindi a $Δy$ in quanto
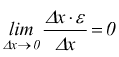
Il termine f'(x) ·Δx viene chiamata parte principale dell'infinitesimo Δy e viene chiamato differenziale di y=f(x) e indicato con dy:
![]()
Il differenziale di una funzione è uguale al prodotto della derivata della funzione per l'incremento della variabile. Se è f(x)=x si ha
![]()
L'incremento della variabile è uguale al differenziale della variabile. Allora si può scrivere:
![]()
Il differenziale di una funzione è uguale al prodotto della derivata della funzione per il differenziale della variabile. Dalla precedente si ricava
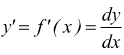
Con locuzione imprecisa, si dice che la derivata è il quoziente di due differenziali; sottintendendo il passaggio al limite per tale quoziente, dato che i termini della frazione sono infinitesimi e come tali ha solo senso parlare del limite del loro quoziente.
 edutecnica
edutecnica