Crittografia a chiave privata (simmetrica)

      

La crittografia è una tecnica usata per rendere visibili le informazioni solo alle persone a cui sono destinate. Il messaggio che può essere letto da tutti si chiama testo in chiaro.
Tramite i metodi di cifratura (algoritmi di codifica) si trasforma il testo in chiaro in un testo cifrato in cui l'informazione viene resa illeggibile.
L'operazione inversa viene chiamata decifrazione (eseguita tramite algoritmi di decodifica) serve per ricomporre il testo in chiaro a partire dal testo cifrato.
La codifica e la decodifica sono eseguite dagli algoritmi crittografici assieme ad una chiave che di solito è un numero molto grande .

La crittografia è stata usata fin dall'antichità; è noto ad esempio, il codice di Giulio Cesare che durante le battaglie, spediva dispacci usando simboli alfabetici che differivano di una costante (chiave) dall'alfabeto naturale.

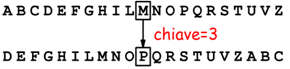
In questo modo tutte le ricorrenze della lettera A nel testo vengono sostituite dalla lettera D; quelle della lettera B con la lettera E. La parola GIULIO CESARE verrebbe codificata come LNAONR FHVDUH.
Il codice di Cesare è già stato oggetto di studio nell'esercizio no.3 di questa pagina.

Questo tipo di codice viene chiamato anche cifrario a sostituzione; ovviamente il numero di chiavi possibili è molto limitato e la possibilità che la chiave possa essere dedotta è elevato. L'algoritmo di Giulio Cesare non è dunque un cifrario sicuro: esso può essere violato facilmente anche senza conoscere la chiave.

Un altro sistema di crittografia è il cifrario a trasposizione in cui la chiave è una parola che serve per spezzare il messaggio su più righe e successivamente per ordinare le colonne risultanti ottenendo il testo cifrato.

Supponendo di voler crittare il seguente
messaggio:AVANZARE FINO AL FIUME
usando la parola
chiave:CAMPO

si crea una tabella con un numero di colonne uguale al numero di caratteri della parola chiave, e si posiziona sulla prima riga la parola chiave. I caratteri del messaggio vengono distribuiti sulle righe sottostanti, sotto ogni lettera della parola chiave.

C	A	M	P	O
A	V	A	N	Z
A	R	E	F	I
N	O	A	L	F
I	U	M	E	.

Se l'ultima riga non è completa, si aggiungono dei caratteri di riempimento ( ad es.il punto . ) il messaggio cifrato viene generato prendendo le colonne della tabella seguendo l'ordine alfabetico

A

C

M

O

P

V

R

O

U

A

A

N

I

A

E

A

M

Z

I

F

.

N

F

L

E

messaggio cifrato:VROU AANI AEAM ZIF. NFLE Il destinatario del messaggio conoscendo la parola chiave è in grado di ricomporre il testo in chiaro individuando le colonne e posizionandole in modo corretto nella tabella.
Alcuni aspetti della cifratura per trasposizione erano già stati visti in precedenza.

Oltre alla crittografia si è anche sviluppata l'opposta crittoanalisi che ha la funzione di analizzare e violare le comunicazioni cifrate.
Un criterio fondamentale della crittografia stabilisce che la sicurezza di un sistema informatico deve dipendere solo dalla chiave e non dell'algoritmo usato.

Basandosi su questa filosofia si è successivamente arrivati ad implementare cifrari di tipo one-time pad dove si utilizza un blocco(pad) di chiavi che vengono generate casualmente che cambiano ad ogni lettera.

Lo sviluppo di queste tecniche ha portato al giorno d'oggi alla creazione di generatori di chiavi 'usa e getta' soprattutto nel settore delle transazioni bancarie ( o-key ).

La chiave utilizzata può essere interpretata come un numero molto grande e la sua dimensione viene misurata in un numero di bit: più grande è la chiave e più difficile sarà il compito di chi vuole infrangere i messaggi cifrati.

Una chiave di 40 bit è ritenuta abbastanza sicura, perché chi volesse decifrare i messaggi dovrebbero cercare tra 2⁴⁰ possibili chiavi.
Un sistema crittografico a chiave simmetrica molto conosciuto è il DES ideato nel 1976 dalla IBM, tuttora usato per cifrare files nei personal computer.
Questo sistema utilizza una chiave di 56 bit (2⁵⁶ possibili chiavi)e per lungo tempo è stato ritenuto piuttosto sicuro anche se si poteva già ipotizzare una sua possibile vulnerabilità dovuta al progressivo aumento delle prestazioni dei calcolatori .
Infatti il DES fu violato nel 1998.

Nel 1997 è stato quindi organizzato, dal dipartimento di commercio americano (NIST) un concorso per sostituire l'ormai insicuro DES e definire un nuovo standard crittografico.

Risultò vincitore del concorso l'algoritmo Rijndael : esso rispettava praticamente tutti i canoni richiesti dal NIST risultava inoltre, essere resistente a tutti gli attacchi a un costo computazionale relativamente modesto.
L'implementazione informatica di Rijndael fu chiamata AES e fu progettato sulla base di tre specifiche fondamentali:
— resistenza contro tutti gli attacchi;
— velocità e compattezza del codice su un'ampia gamma di piattaforme
— semplicità progettuale

AES è stato il primo standard approvato da NSA per comunicazione crittate ed è tuttora il cifrario a chiave segreta più usato negli ambienti informatici: a oggi non sono conosciuti attacchi in grado di violarlo in tempi accettabili.

Il punto debole della crittografia simmetrica rimane, comunque, il fatto che i due interlocutori devono essere in possesso della stessa chiave.
Questo limite può essere superato solo con l'uso della crittografia asimmetrica dove non è necessario concordare le chiavi di cifratura.

Crittografia a chiave pubblica (asimmetrica)

      

L'idea alla base della crittografia asimmetrica è quello di avere due chiavi diverse, una pubblica per la criptazione e una privata per la decriptazione, che deve essere mantenuta segreta.
Fra due interlocutori, non vi è dunque la necessità di scambiarsi le chiavi.
Una opzione possibile è la seguente :

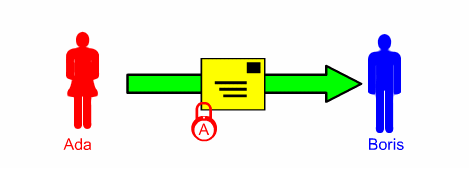
1 ] Ada manda a Boris il messaggio contenuto in una scatola chiusa con un lucchetto: né Boris né eventuali intrusi possono aprirlo;

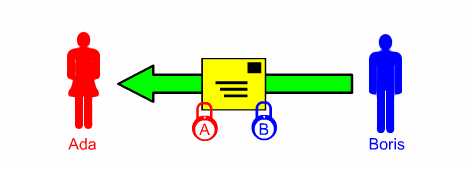
2 ] Boris lo rispedisce ad Ada aggiungendo un suo lucchetto B: nessuno ora è in grado di aprirlo;

3 ] Ada toglie il suo lucchetto e rimanda il pacco a Boris, che ora ha solo il suo lucchetto e che alla sua ricezione può aprirlo e leggere il messaggio.

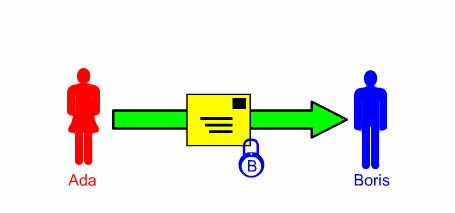
Come si vede Ada e Boris non si sono scambiati le chiavi ( e non hanno una chiave in comune) , però la procedura è piuttosto macchinosa perché ci sono 3 trasmissioni; un'altra opzione è la seguente:

1 ] Boris manda ad Ada il proprio lucchetto aperto e questa lo conserva fino a che ha neccesità di spedire qualcosa a Boris

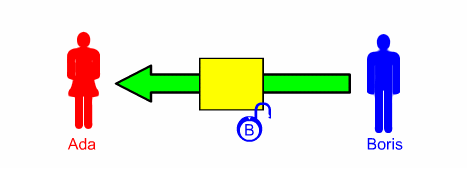
2 ] Quando Ada deve spedire un messaggio a Boris, lo chiude con il suo lucchetto e glielo invia: senza il triplo invio del messaggio e ci siamo riportati nella situazione descritta in precedenza.

La chiusura del lucchetto viene effettuata con una determinata chiave pubblica che ciascun utente mette a disposizione di tutti gli altri utenti che necessitano di trasmettergli messaggi: la chiave privata è invece segreta, in possesso a ogni utente, che la utilizza per "aprire" il lucchetto e leggere il messaggio.

Formalmente è necessario trovare una funzione (il lucchetto) la cui trasmissione su canali insicuri non comprometta l'algoritmo, che sia facile da computare ( parte pubblica che chiude il lucchetto ) ma difficile da invertire ( parte privata che apre il lucchetto ).

Algoritmo Diffie-Hellman

      

Si tratta di un algoritmo, elaborato nel 1976, che realizza un sistema di crittografia basato sullo scambio di chiavi. Premesso che con la scrittura : r=x mod y intendiamo il resto della divisione fra due numeri interi
x ed y (come verrà poi specificato meglio) . Considerando il problema di comunicazione dei due soggetti menzionati in precedenza, bisogna disporre di un numero g : generatore e un numero primo p.

Ada sceglie un numero casuale a e calcola A=g^a mod p
e lo invia attraverso il canale pubblico a Boris assieme a g e a p.

Boris sceglie un numero casuale b e calcola B= g^b mod p
e lo invia ad Ada che calcola K_A= B^a mod p, mentre Boris calcola K_B=A^b mod p.

A questo punto i due interlocutori sono in possesso della chiave segreta e possono cominciare ad usarla per cifrare le comunicazioni successive. Un attaccante può benissimo ascoltare tutto lo scambio ma per calcolare i valori di a o b avrebbe bisogno di risolvere l'operazione di logaritmo discreto che è computazionalmente onerosa e richiede parecchio tempo in quanto sub-esponenziale.

I valori calcolati sono gli stessi dato che B^a=g^ba e A^b=g^ab. Supponiamo p=23 e g=5 .

Ada sceglie a=2 e calcola A= g^a mod p=5² mod 23=25 mod 23=2
Boris sceglie b=3 e calcola B= g^b mod p =5³ mod 23=125 mod 23=10

Boris spedisce B ad Ada e Ada spedisce A a Boris

Ada calcola K_A=B^a mod p=10² mod 23=100 mod 23=8
Boris calcola K_B=A^b mod p=2³ mod 23=8 mod 23=8

stessa chiave segreta.

Si può già dire che l'algoritmo Diffie-Hellman introduce il concetto di crittografia asimmetrica che verrà poi implementato compiutamente dall'algoritmo RSA di cui è precursore.

Algoritmo RSA

          

Questo meccanismo è implementato negli algoritmi di crittografia asimmetrica, come ad esempio nell'algoritmo RSA (dal nome dei suoi creatori Rivest, Shamir e Adleman).

La teoria RSA è costituita da alcuni specifici ingredienti matematici: il teorema di Fermat, l'algoritmo di Euclide esteso per il calcolo dell'MCD , le proprietà di primalità fra i numeri interi e una buona quantità di algebra modulare.
Per quest'ultima è necessario far mente locale ad alcune nozioni usualmente introdotte alle scuole primarie.
S se m è un intero con m>0, ogni intero b si può scrivere nella forma :

stiamo infatti eseguendo la divisione:

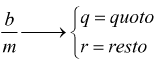
e questa scrittura è unica se si vuole 0 <= r < m,
r è dunque l'unico intero compreso tra 0 ed m tale che ( b-r ) sia divisibile per m:
r, si chiama resto di b modulo m e si scrive:

r = b mod m

e lo si calcola con l'operazione r=b-m*int(b/m).

E' equivalente dire che due interi hanno lo stesso modulo m oppure che differiscono per un multiplo di m e sono ovvie le identità

0 mod m=0
1 mod m=1

Teorema RSA:
Siano p e q sono due numeri primi distinti e n = p·q se e è coprimo ad m=(p-1)(q-1) ed è tale che
e·d = 1 mod n, allora per ogni a ∈ N si ha a^ed =a mod n .

Questa è solo la definizione del teorema che però, prevede alcuni presupposti matematici: è noto che se due numeri p e q sono primi fra loro si ha MCD(p,q)=1.
Per questo basta usare l'algoritmo di Euclide per il calcolo rapido dell'MCD fra due numeri

int euclide(int a,int b){
if(b){
   while(b){
       r = a%b;
       a=b;
       b=r;
    }
return a;
}

L'algoritmo, pur essendo stato inventato ai tempi di Euclide, funziona ancora molto bene

a

  b

In pratica , nell'applicazione dell'algoritmo RSA, devono essere ricavati i seguenti elementi:

Il primo passo è la generazione delle chiavi si scelgono due numeri primi p e q tali che

n = p·q

poi si pone

m=(p-1)·(q-1)

viene in seguito SCELTO l'esponente pubblico: e coprimo di m cioè e è un numero primo e soddisfa la relazione e < m se due numeri sono coprimi fra loro si ha MCD(e,m)=1 .
si calcola d in modo che venga soddisfatta la relazione

d·e=1 mod m

cioè il resto della divisione fra (ed)/m è 1.

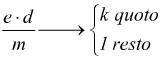               quindi si può scrivere                 

da cui si può ricavare       ovviamente k∈N cioè k deve appartenere all'insieme N dei numeri naturali. Riassumendo:

a ] scelgo una coppia di numeri primi p e q
b ] ottengo n=p·q
c ] calcolo m=(p-1)(q-1)
d ] scelgo e < m coprimo di m [ e ed m non sono divisibili fra loro MCD(e,m)=1 ]
e ] ottengo d dalla relazione d·e=1 mod m ( cioè il resto della divisione fra ed/m è 1 )
f ] verifico il risultato ottenuto con la relazione d=(km+1)/e con k numero intero.

Esempio

p=3
q=11
n=p·q=3·11=33
m=(p-1)(q-1)=(3-1)(11-1)=20

scelgo un numero coprimo di m tale che MCD(e,m)=1 .
SCELGO e =7 < 20 . Poi devo applicare la regola : d·e=1 mod m
cioè il resto della divisione fra ed/m è 1.
il resto della divisione fra 7d/20 deve essere 1
può essere d=3 perchè 7·3/20 ha come resto 1
( il 20 sta nel 21 1 volta con l'avanzo di 1)

oppure osservando l'equazione con k∈N  si fa crescere k finchè d non assume un valore intero :

d=(k20+1)/7
infatti per k=1 si ha d=21/7=3 .

Se non si vuole procedere a tentativi per il calcolo di d, dobbiamo ricorrere alla funzione di eulero ɸ(n) definita come

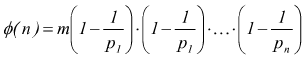
dove p₁ , p₂ ,.., p_n sono i divisori primi di m (presi una sola volta). Nel caso in esame m=20=2·2·5;dunque

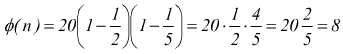
poi si trova d con la formula     cioè

I numeri p e q tali che n=pq e che generano le coppie (e,n) e (d,n) sono conosciuti come numeri RSA.
Non è possibile risalire facilmente dalla chiave pubblica e quella privata (e viceversa), in quanto servirebbe conoscere il numero (p-1)(q-1) e questo implica fattorizzare n nei suoi fattori p e q che è un problema computabilmente difficile.

Codifica

Il messaggio m da trasmettere deve essere espresso in forma numerica ; numericamente deve essere m < n. Se il messaggio è alfanumerico, ogni lettera dell'alfabeto può essere associata ad un numero, ad es. A=1, B=2 etc.. Il crittogramma cod viene codificato calcolandolo come

cod= m^e mod n ( risulta c < n )

Volendo trasmettere il messaggio msg=9 con le chiavi precedenti, pubblica (7,33) e privata (3,33) otteniamo:

msgx=9⁷ mod 33 =4782969 mod 33=15

ovviamente, msgx è il codice cifrato del messaggio originale in chiaro che chiamiamo msg.

Decodifica

La decifrazione del messaggio avviene calcolando

msg=msgx^d mod n

Utilizzando come chiave privata (33,7) otteniamo:

msg=15³ mod 33= 3375 mod 33=9

Una implementazione rapida di questo algoritmo è qui sotto riportata

p :    q :    msg : A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

  

e :