Data l'equazione di II° grado ax²+bx+c=0 dove a,b,c sono numeri reali qualsiasi scrivi la procedura e descrivi il suo diagramma di flusso tenendo conto dei seguenti casi:
1) a≠0 b e c qualsiasi
2)a=b=0 c≠0
3)a=b=c=0
4)a=0 b≠0 c qualsiasi.
Per ciascuno dei casi indicati la procedura deve condurre alla determinazione delle soluzioni o alla segnalazione di situazioni singolari (indeterminata, impossibile, etc..)

Si distinguono i due casi principali dove a≠0 ed a=0 in quest’ultimo caso l’equazione si riduce a: bx+c=0 che fornisce come soluzione x=-c/b in questo caso avremo:

1) b=c=0 l’eq. si riduce ad una identità 0=0 la risposta sarà cout << "identità" .
2) b=0 c≠0 ne segue che x=-c/0=infinito la risposta sarà cout << "impossibile".
3) b≠0 c=0 ne segue che x=-0/b la risposta sarà cout << 0 oppure cout << -c/b.
4) b≠0 c≠0 la risposta sarà cout << -c/b:

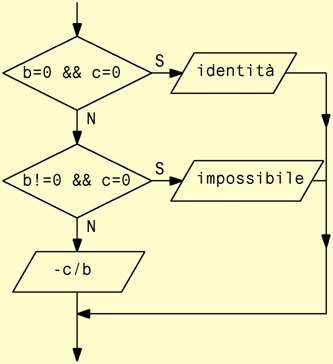
Alla luce delle considerazioni precedenti il diagramma a blocchi del ramo a=0 può essere illustrato come in figura.
Nel caso a≠0 basterà automatizzare la procedura con la formula risolutiva del trinomio di II°grado; allo scopo verrà usata la variabile d (discriminante) con:
d=b*b-4*a*c
se d≥0 allora si può usare la formula risolutiva
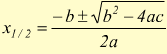    che in linguaggio C viene scritta come:
X1=(-b+sqrt(d))/(2*a)
X2=(-b-sqrt(d))/(2*a)

Se d<0 non vi sono soluzioni in campo reale e quindi la risposta sarà: cout << "impossibile".

si viene ad ottenere il seguente codice sorgente:

#include<iostream>
#include<math.h>
using namespace std;
main(){
float a,b,c,d;
cout<<"a:";cin>>a;
cout<<"b:";cin>>b;
cout<<"c:";cin>>c;
if(!a){
     if(!b && !c)cout<<"identità";
     else if(!b && c)cout<<"impossibile";
     else cout<<-c/b;
     }
else{
d=b*b-4*a*c;
if(d<0)cout<<"-impossibile-";
else {
     cout<<(-b+sqrt(d))/(2*a)<<" ";
     cout<<(-b-sqrt(d))/(2*a);
     }
}//fine if(!a)
}//fine main