Esercizio 8                     

Dato un insieme A di n uomini e un insieme B di n donne, assegnare ciascuno degli n uomini a ciascuna delle donne in modo che ogni soluzione sia priva di instabiltà; un matrimonio viene ritenuto stabile se ciascun uomo che preferisce un'altra compagna a quella che gli ha assegnato l'algoritmo è già stato rifiutato precedentemente da ella (che evidentemente gli preferisce un altro).
Utilizzare una LinkedList per tenere traccia degli uomini non sposati.

---

L'algoritmo dei matrimoni stabili è un classico dei problemi di assegnazione: siano A e B due insiemi dotati di uguale cardinalità n, si trovi un insieme di coppie < a,b > tali che a in A e b in B soddisfino una condizione data. Si possono stabilire vari criteri di selezione; uno di questi viene denominato la 'regola del matrimonio stabile'.

Si assume cha A sia un insieme di n uomini e B un insieme di n donne e che tutti abbiano dichiarato le proprie preferenze in materia di compagni di coppia. Se le n coppie vengono assegnate in modo tale che esistono un uomo e una donna che si preferiscono reciprocamente al posto dei propri promessi sposi allora si dice che gli assegnamenti dati sono instabili.
Se tale coppia non esiste, allora gli assegnamenti sono detti stabili.

Si tratta di un algoritmo di scelta ottima e come nel caso dell'algoritmo delle otto regine può essere risolto con tecniche di backtracking (procedendo a tentativi).
Si nota come possa essere applicato a diversi problemi analoghi ( di tipo associativo ) come ad esempio la scelta di un ospedale da parte di un medico, oppure la scelta di una scuola da parte degli studenti oppure la scelta delle reclute da parte di diverse forze armate, ma come già detto va applicato fra due insiemi costituiti ciascuno da n elementi.

Una possibile strategia consiste nel costruire iterativamente le coppie, determinando per ogni uomo la sua compagna grazie ad un sistema di offerte successive: l'uomo chiede di associarsi alla donna che preferisce , ma se questa gli preferisce il compagno attribuitole durante i passi precedenti dall'algoritmo, l'uomo la cancella dalla sua lista e si propone a quella successiva; se invece la donna preferisce lui al proprio compagno attuale (oppure se è ancora nubile) l'uomo le viene ( almeno provvisoriamente ) assegnato e l'eventuale compagno che lei ha rifiutato torna in circolazione per cercare la successiva donna della sua lista e il giro avrà termine appena si arriva ad una donna sola oppure a una donna che lo preferisce rispetto al suo attuale compagno.

Chiaramente, servono delle strutture di dati per definire, almeno all'inizio, le preferenze dei vari soggetti.
Per avere una idea, supponiamo di avere n=5 con gli uomini rappresentati da una lettera inscritta in un quadrato e le donne rappresentate da dei numeri inscritti in un cerchio:

Da cui si capisce che l'uomo A preferisce in ordine la donna 2 poi la 5, la 1 ..etc. La donna 1 preferisce in ordine discendente l'uomo E poi A,D,B ed infine C.
Un set di matrimoni è instabile se due soggetti non sposati preferiscono entrambi altri soggetti ai loro promessi sposi. Si vede, inoltre come le assegnazioni 1A 3B 2C 4D 5E sono instabili, perché A preferisce 2 a 1 e 2 preferisce A a C; succederebbe che A lascia 1 per 2 e 2 lascia C per A.

Se l'algoritmo funzionasse dovrebbero accadere i seguenti eventi:


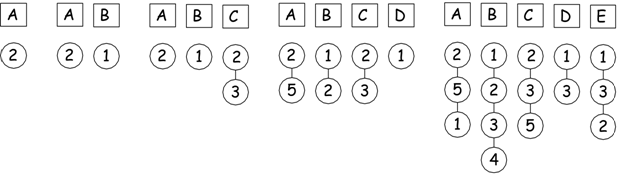
I primi due passaggi sono privi di problemi perché ciascun uomo sceglierebbe la donna che gli interessa; quando si inserisce C, esso tenterà di associarsi alla donna 2 in quel momento accompagnata all'elemento A, ma non riesce a farlo perché nella lista delle preferenze della 2, A risulta preferibile a C, quindi C sceglierà l'elemento successivo nella sua lista cioè la donna 3 in quel momento libera.
Al quarto passaggio si inserisce l'elemento D che può associarsi alla donna 1 che precedentemente stava con B: può farlo perché nella lista di 1, D ha la priorità su B. B ritorna dunque libero puntando alla donna 2 (che prima stava con A) che nella sua lista viene immediatamente dopo 1, riesce in questa operazione perché nella lista di 2 B ha priorità su A??.in pratica si va aventi secondo questa logica; alla fine avremo se seguenti associazioni:

quindi l'elenco finale dei matrimoni sarebbe
D+U
0+0
1+4
2+3
3+2
4+1

I dati precedenti verrebbero codificati in due matrici
int pref[][]={//tabella preferenze degli uomini
   {1,4,0,2,3},
   {0,1,2,3,4},
   {1,2,4,3,0},
   {0,2,1,3,4},
   {4,2,1,0,3}
};
int rango[][]={//tabella preferenze delle donne
   {4,0,3,1,2},
   {3,4,1,0,2},
   {0,3,1,2,4},
   {2,1,3,0,4},
   {3,1,2,4,0}
};
vengono dichiarate le variabili
int i,u=0,d=0,n=5;
i=contatore u rappresenta un generico uomo, d una generica donna.
n è il valore più importante: di quanti elementi sono costituiti gli insiemi.

Poi,per ogni donna, dobbiamo sapere chi è il suo attuale fidanzato:.
int fida[]= new int[n];
cioè fida[d] ci indica l'uomo u fidanzato alla donna d.
Tutti gli elementi di questo vettore vengono inizializzati a -1 per specificare che inizialmente nessuna donna è accompagnata.

Poi per sapere quali uomini non sono attualmente impegnati usiamo una linkedlist di interi .
LinkedList < Integer > lista = new LinkedList < Integer > ();
essa viene inizializzata con gli indici identificativi degli uomini.
Inoltre, abbiamo bisogno di tenere traccia di quanto ogni uomo è avanzato sulla sua lista. Questo può essere considerato attraverso il vettore next[ ].
next[u] indica la donna attuale, next[u]++ è l'indice della prossima donna nella lista di preferenze dell'uomo u.
Il ciclo while deve continuare finchè nella lista ci sono uomini non accompagnati; esso è costituito da due parti; nella prima si valuta se la donna che arriva per prima nell'elenco non è accompagnata; se non lo è viene assegnata all'uomo attuale. Nella seconda si chiama il metodo statico scelta per valutare se il rango dell'uomo considerato può scavalcare il rango dell'uomo attualmente accompagnato alla donna d. Se questo avviene si deve procedere ad uno scambio attraverso la variabile ausiliaria t, mentre torneranno nella lista degli uomini liberi o il soggetto attuale .
lista.add(u);
o il suo ex fidanzato:
fida[d] = u;
lista.add(t);
alla fine di tutte queste iterazioni (potrebbero essere parecchie) quando gli elementi della LinkedList si sono esauriti, si stampa la configurazione finale attraverso il metodo
stampaMat(fida);
Ovviamente, la soluzione ottenuta è priva di instabilità: se un uomo alla compagna che gli ha assegnato l'algoritmo preferisce un'altra donna, ma da questa, egli è già stato rifiutato.