Macchina asincrona
La macchina asincrona può funzionare come motore o come generatore; come
motore ha un vasto campo di impiego, grazie alla sua semplicità di applicazione,
come generatore ha un utilizzo invece piuttosto raro.
Essa viene alimentata da un sistema polifase (perchè tale è la distribuzione
dell' energia).
E' costituito da due parti, una fissa: lo statore e una mobile: il rotore.
Sullo statore vengono disposte un certo numero di coppie di bobine opposte fra loro. Disponendo 'p' coppie di bobine (coppie di poli) sfasate nello spazio e alimentandole con correnti sfasate nel tempo si genera un campo magnetico rotante all'interno dello statore.
Sotto è riportato un motore a 6poli=2p (con p=3 coppie di poli sfasate fra loro di 120°).
Il circuito rotorico può essere costituito da 'p' circuiti chiusi in cortocircuito, dove sotto l'effetto del campo magnetico rotante viene indotta una corrente circolante. Ciascuno di questi circuiti viene denominato fase rotorica.

La corrente indotta in ciascuna fase rotorica crea a sua volta un campo
magnetico rotante con senso opposto a quello dello statore se il polo
del rotore e quello dello statore sono dello stesso tipo, essi si respingono
e il rotore si mette in moto.
Il rotore non può, comunque, ruotare alla ruota alla stessa velocità dello
statore ma è sempre più lento, a causa del carico, e degli attriti meccanici
cui va incontro col suo movimento.
La velocità relativa Δω tra il campo rotante che ruota a velocità ω0 e il rotore che ruota alla velocità ω 1 è:
![]()
viene definito lo scorrimento
come il rapporto (adimensionale)

Inoltre, se ω è la pulsazione della rete di alimentazione,risulta:
 [rad/s] ;
[rad/s] ;  [giri/min]
[giri/min]
ωr è dunque la velocità angolare relativa del rotore rispetto al rotore; essa induce nell'avvolgimento rotorico una corrente di frequenza:
$$f_r=ω_r/{2π}$$ ovviamente se $$s=ω_r/ω_o \; ⇒\; ω_r=sω_o$$ quindi :
![]() frequenza
(elettrica) della corrente rotorica
.
frequenza
(elettrica) della corrente rotorica
.
in analogia possiamo scrivere ![]()
indicando con E20 il valore di E2 (tensione ai capi
dell'avvolgimento rotorico secondario) durante il funzionamento a rotore
bloccato (rotore fermo s=1). Allo spunto s=1 e la frequenza della corrente
rotorica coincide con quella del campo; poi ovviamente sapendo che :


 [giri/min] velocità
(meccanica) del rotore
[giri/min] velocità
(meccanica) del rotore
allo spunto s=1 e conseguentemente n1=0 (il rotore è fermo
: la sua velocità e nulla)
dalla meccanica sappiamo che $$ω={2πn}/60\;⇒\;2πf={2πn}/60\;⇒\;f=n/60$$
o anche $n=60f$ per
cui: $$n_1=60f_1\;⇒\;60f_1=60f/p(1-s)$$ cioè:
 [Hz]
frequenza (meccanica) del rotore con f= frequenza di rete
[Hz]
frequenza (meccanica) del rotore con f= frequenza di rete
è ovvio che se s=1 deve essere nR=0 quindi il rotore è fermo.
Se s=0 deve essere nR=nS il motore funziona alla
velocità di sincronismo del campo magnetico statorico. In genere s varia
dal 1% al 5%.
In tabella sono indicate le velocità in giri/min in funzione delle coppie
di poli:
|
coppie di poli |
Velocità in g/min a 50Hz |
|
1 |
3000 |
|
2 |
1500 |
|
3 |
1000 |
|
4 |
750 |
|
5 |
600 |
|
6 |
500 |
Essendo la struttura del motore sempre simmetrica, indipendentemente , dal numero di fasi, sarà sufficiente studiarne una sola, per ottenere delle informazioni complessive sulla macchina. Il circuito equivalente di ogni singola fase è illustrato nella seguente figura:

Rispetto al circuito equivalente del trasformatore ci sono le seguenti differenze:
1] La frequenza rotorica è diversa da quella statorica ed è variabile
con lo scorrimento.
2] Il motore non alimenta un carico elettrico sul secondario, dato che
le fasi rotoriche sono chiue in corto circuito.
3] Alimentando il motore con una terna simmetrica di tensioni, esso si
comporta sempre come un carico equilibrato e quindi per descrivere il
suo funzionamento basta considerare quello che avviene in una fase.
L'impedenza primaria statorica, Z1=R1+jX1 tiene conto della resistenza e della reattanza di dispersione di ogni fase.
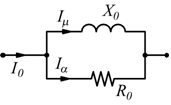
L'ammettenza Y0=G0-jB0 raggruppa i parametri trasversali G0 e B0 tenendo conto delle perdite nel ferro (I0) e dalla potenza reattiva magnetizzante (Iµ).

Il trasformatore ideale con rapporto di trasformazione E1/E2 di accoppiamento fra il circuito rotorico e statorico; essendo E2 variabile con lo scorrimento,anche tale valore rapporto di trasformazione dipenderà da s.
L'impedenza rotorica Z2=R2+jsX2 (dove la parte immaginaria dipende da s).
Dato che E2=sE20 abbiamo:


In questo modo il circuito secondario (rotorico) può essere visto come:

Infatti: $$R_2+R_2{1-s}/s=R_2+R_{2s}/s-R_2=R_2/s$$
R2 è la resistenza propria della fase rotorica mentre $$R_2{1-s}/s$$ può essere vista come una resistenza fittizia che rappresenta il carico meccanico. Poi si ha:
 Potenza
elettrica trasmessa
Potenza
elettrica trasmessa
![]() Potenza
persa nell'avvolgimento rotorico (perdita nel rame relativa ad una fase.
Potenza
persa nell'avvolgimento rotorico (perdita nel rame relativa ad una fase.
 Potenza
meccanica totale fornita all'albero meccanico, somma della potenza meccanica
utile e della potenza meccanica persa per attrito e ventilazione.
Potenza
meccanica totale fornita all'albero meccanico, somma della potenza meccanica
utile e della potenza meccanica persa per attrito e ventilazione.
 e
e 
 cioè:
cioè: ![]()
Queste considerazioni confermano la possibilità di introdurre nel circuito equivalente la:
 Resistenza
di carico
Resistenza
di carico
Si ha, quindi, il circuito equivalente completo:

Esso ha il vantaggio di usare un trasformatore ideale con K0
fisso non dipendente da s e pari al rapporto di trasformazione a rotore
bloccato.

Bilancio delle potenze
![]() Potenza
assorbita
Potenza
assorbita
Le perdite nel ferro valgono $P_f=3G_0E_1^2$ ma $$E_1=V_{1f}^2/√3$$ da cui $$P_f=3G_0(V_{1f}/√3)^2$$
![]() Perdite
nel ferro (trascurabili nel funzionamento a carico)
Perdite
nel ferro (trascurabili nel funzionamento a carico)
![]() Perdite
nel rame statoriche
Perdite
nel rame statoriche
 Perdite
addizionali statoriche
Perdite
addizionali statoriche
![]() Potenza
trasmessa al rotore (ricordarsi che $$P_T=3R_2/sI_2^2$$ )
Potenza
trasmessa al rotore (ricordarsi che $$P_T=3R_2/sI_2^2$$ )
Si nota che ![]() (importante)
(importante)
$P_m=P_T-P_{j2}$ Potenza meccanica a cui si deve ulteriormente sottrarre PAV, cioè le perdite per attrito e ventilazione.


Macchina asincrona prova a vuoto

Il motore funziona a vuoto
quando non vi è carico meccanico collegato all'albero.
L'avvolgimento statorico è alimentato con tensione V1 e assorbe
una I0 di intensità ridotta rispetto alla I1 nominale.
In pratica la corrente assorbita I1=I0. Le fasi
rotoriche sono in circuito aperto, come nel trasformatore in cui il secondario
a vuoto è aperto. Questo perchè a vuoto s=0; idealmente n0=n1
.
Al movimento del rotore si oppongono solo gli attriti e manca la coppia resistente del carico. La velocità del motore è prossima a quella di sincronismo. In queste condizioni:
![]()
Nel caso ideale: $s=0\; ⟶\; R_m=∞$
![]()
![]()
![]()
![]()
![]() quindi:
quindi:
![]() essendo
essendo ![]()
le perdite addizionali PADD sono quatificabili come il 5% della P0.
Macchina asincrona funzionamento a rotore bloccato
Si ha quando il rotore è fermo, la velocità è nulla e s=1. In pratica si verifica all'istante iniziale dell'avviamento. E' anche indicato come funzionamento di corto circuito (locuzione ambigua,dato che le fasi rotoriche sono collegate in corto anche durante il funzionamento normale).


Si ha:  Corrente
rotorica di corto circuito
Corrente
rotorica di corto circuito
Dato che:  con
con

ma è I'2cc>>I0 bisogna trascurare l'ammettenza Y0.
Si può usare una proprietà importante del trasformatore: la trasformazione di impedenze.
 Riportiamo
le grandezze dal secondario al primario:
Riportiamo
le grandezze dal secondario al primario:

Si può anche effettuare il riporto delle grandezze dal primario al secondario:

A questo punto avremo:

cioè:


che è il circuito equivalente statorico a rotore bloccato.
Con:
 Corrente
di avviamento o corrente di spunto
Corrente
di avviamento o corrente di spunto
In questo caso $P_U=P_{AV}=0\;⇒\;η=0$ dato che il rotore è bloccato.
![]() perdite
nel rame statoriche
perdite
nel rame statoriche
si ha inoltre $P_f=G_0V_{1f}^2$ e $$P_{ADD}={0,5}/100P_A$$
![]() potenza
assorbita a rotore bloccato (PU=0; η=0)
potenza
assorbita a rotore bloccato (PU=0; η=0)
Nella prova a rotore bloccato si alimenta
il motore a tensione ridotta in modo da far circolare una corrente pari
a quella nominale I1n.
In analogia con la prova di cortocircuito di un trasformatore si usa una
V1CC con la I1n.
Nella prova a rotore bloccato, essendo bassa la V1CC si possono
trascurare Pf = 0 e PADD = 0.
Si ha inoltre:
$P_A=P_j$ cioè potenza assorbita=perdite nel rame; si ha poi $P_j=P_{ccn}=3R_{1cc}I_{1n}^2$

 oppure
oppure

Macchina asincrona:circuito equivalente semplificato

Semplificando

Semplificando ulteriormente




Caratteristica meccanica di una macchina asincrona
Bisogna ricordarsi la formula fra coppia, potenza e velocità angolare:

Per il calcolo della coppia, considero sempre CT (coppia elettromagnetica
trasmessa).

avendo indicato con p, il numero di coppie polari e sapendo che $P_{j2}=3R_2I_2^2$
perdite
rotoriche nel rame, quindi avremo:

Dal circuito equivalente semplificato avremo:

n.b.:

![]()

abbiamo detto che  con
con ![]() quindi:
quindi:


evidentemente : CT=CT(s) cioè CT dipende da s. Ricordiamo che s=1 all'avviamento.

Si ha un massimo in sCR (scorrimento critico)
 dato
che
dato
che ![]()
possiamo notare che:

in corrispondenza dello scorrimento critico si ha la coppia massima:

All'aumentare della resistenza rotorica, aumenta lo scorrimento critico
mentre diminuisce la velocità critica.

Per nCR
Per n1
Avviamento


allo spunto (avviamento)  quindi:
quindi:

All'aumentare della velocità, lo scorrimento si riduce , la resistenza
equivalente del rotore R2/s aumenta e la corrente assorbita
dal motore diminuisce.
Affinché un motore possa avviarsi e sviluppare una certa accelerazione
angolare iniziale la coppia di avviamento del motore deve essere maggiore
della coppia resistente di avviamento del carico meccanico.


Come si nota nel primo caso: CA<CRA (coppia resistente all'avvio) : il motore non si avvia. Nel secondo: CA>CRA il motore si avvia e il funzionamento si stabilizza in P.
 edutecnica
edutecnica