Calcola la capacità equivalente vista tra i morsetti A e B del circuito di figura e la carica totale dell'armatura equivalente quando sia applicata una tensione VAB=120V C1=160pF C2=0,2nF C3=21,1pF C4=0,25nF [ CT=76,4pF | Q=9,168nC ]
Nel circuito illustrato, con: E=60 V R=10 Ω R1=6 Ω R2=40 Ω C=6 µF Trova la carica localizzata sulle armature del condensatore C. [ Q=288·10-6 C ]
Nel circuito illustrato, i valori sono: C1=8 µF C2=12 µF C3=20 µF C4=5 µF Calcola la capacità equivalente, vista fra i nodi A e B e quindi quella vista tra i nodi B e D. [ CAB=29,8µF | CBD=18µF ]
Due condensatori sono collegati come illustrato in figura: per ottenere una ripartizione della tensione Vi applicata in ingresso. Sono noti Vi=200 V C1=0,8 µF V2=40 V. Trova il valore della capacità del condensatore C2 che permette di ottenere la ripartizione di tensione desiderata ed il valore della capacità del condensatore C3 da porre in parallelo a C1 in modo che la tensione di uscita si porti a V'2=75 V . [ C2=3,2 µF | C3=1,12 µF ]
Due condensatori: C1=3000pF e C2=4,5nF, vengono posti in parallelo. Calcola la capacità complessiva del parallelo e il valore della capacità di un terzo condensatore C3 da porre sempre in parallelo , in modo che la capacità totale sia di 0,03µF. [CTOT=7,5nF | C3=22,5nF ]
Un condensatore di capacità C, piano, ha le armature di superficie S=500cm2 e distanti fra loro d=4mm; il dielettrico presenta una costante relativa εr=5. Esso viene posto in parallelo con un altro condensatore di capacità pari a (1/3)C. Viene applicata agli estremi del parallelo una tensione di 3000V: Calcola: 1] L'energia elettrica immagazzinata dai due condensatori. 2] La forza di attrazione fra le armature del condensatore C . [U=3,321 10-3 | F=0,83 N]
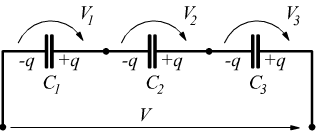
Tre condensatori di rispettiva capacità C1=90pF, C2=25pF, C3=0,04nF, sono collegati in serie e sottoposti alla tensione V=220 V. Calcola: 1] La quantità di carica q su ciascuna armatura. 2] La tensione ai capi di ciascun condensatore. [ 2890,5pC | V1=32,11V | V2=115,62V | V3=72,26V ]
Il partitore capacitivo illustrato ha C2=250pF. Avendo ai capi della serie una tensione di 200 V e volendo ottenere ai capi di C1 una tensione di 40 V, calcolare il valore di C1. [ C1=1 nF ]
Nel circuito rappresentato: i dati sono i seguenti: C1=3 µF C2=2 µF C3=4 µF VAB=300 V Calcola la tensione e la carica elettrica su ogni singolo componente. [V1= 200V | V2=V3= 200V | q1=600µC | q2=200µC | q3=400µC]
Nel sistema di condensatori rappresentato con: C1=12 µF C2=1 µF C3=2 µF C4=3 µF C5=4 µF C6=5 µF C7=18 µF VAB=120 V 1] Calcolare la capacità equivalente fra i morsetti A e B. 2] La carica accumulata su ogni condensatore. 3] La tensione elettrica ai capi di ogni condensatore. [ CAB=10µF | q1=480µC | q7=720µC | q2=80µC | q3=160µC | q4=240µC | q5=320µC | q6=400µC | V1=V7=40V | V2=V3=V4=V5=V6=80V ]
Nel circuito illustrato, considerando VAB=150V: trova la tensione ai capi del condensatore C. [ VC=100V ]
Due condensatori di capacità C1=1,2 μF e C2=3,8 μF sono connessi in serie. La differenza di potenziale ai capi della serie è Vo=100V. I due condensatori carichi vengono separati dalla sorgente di carica e nuovamente collegati tra loro, unendo l'armatura positiva del primo con l'armatura positiva del secondo (dunque in parallelo). Alla fine, quanto vale la differenza di potenziale ai capi della rete di condensatori? Calcola la carica presente alla fine, su ciascuno dei condensatori. Determina la variazione di energia accumulata. [ΔU=1,22·10-3 J]
I tre condensatori all'interno del circuito disegnato hanno capacità C1=1nF C2=2nF C3=3nF. Rispetto a massa si ha VA=20V e VB=80V.Trovare VC. [ 30 V ]
Tra i punti A e B del circuito disegnato viene applicata una differenza di potenziale V. Le capacità dei condensatori sono C1=1nF C2=2nF C3=3nF. Trovare il valore di C4 affinché si abbia VP-VT=0. [ 6 nF ]
Alla rete di condensatori disegnata si applica una differenza di potenziale iniziale V. Si ha C1=C2=25nF e C3=15nF; si ha Q1=5·10-7C. Calcola Q3 sulle armature di C3. In seguito il sistema viene isolato e C1 e C2 vengono riempiti con un materiale di costante dielettrica εr=4. Calcola la differenza di potenziale V1 ai capi del condensatore C1. [ 8,5 V ]
Nello schema C1=2 μF C2=3 μF C3=1,6 μF C4=3,2 μF. La carica sul condensatore C2 è Q2=12·10-5C. Calcola la capacità equivalente del sistema. Determina il valore del potenziale nel punto P e nel punto T. Calcola la carica presente sulle altre armature. [ V P =40 V | V T =100 V]
Un condensatore di capacità C=6,5nF è caricato a V=400V. Il condensatore viene isolato staccandolo dalla sorgente di carica e poi collegato ad un secondo condensatore di capacità Co=2/5C. Determina la differenza di potenziale ai capi dei due condensatori. Calcola la carica immagazzinata su ciascun condensatore. [ 285 V ]
Facendo riferimento al seguente circuito Se C=50 μF, qual è la capacità equivalente tra i punti A e B? Ripetere poi il calcolo tra i punti A e D. [ 40,74 μF | 41,3 μF ]
Nello schema la differenza di potenziale associato alla batteria vale E=10 V e ciascuno dei sette condensatori ha una capacità di 10 μF. Quale è carica su C1 e su C2 ? [ 100 μC | 20μC ]
Nel circuito disegnato si ha: C1=8 μF C2=6 μF C3=8 μF C4=6 μF E=12 V. Quando l'interruttore T è chiuso in modo da collegare C4 , trova quanta carica passa attraverso il punto P dalla batteria e quanta carica elettrica finisce su C4. [ 7,2 μC | 18 μC ]
La differenza di potenziale ai capi della serie è Vo=100V.
edutecnica
edutecnica