Conversione Tensione-Frequenza
La qualità di un segnale analogico è ottenuta misurando il rapporto tra
la potenza del segnale utile e quella del rumore che si sovrappone ad esso
(rapporto segnale-rumore S/N). Tra le cause del deterioramento del segnale
e la seguente perdita di informazione ci sono i disturbi elettromagnetici,
il rumore dei componenti circuitali e le distorsioni dei circuiti e delle
linee di trasmissione.
La grandezza tensione elettrica è particolarmente sensibile a questo tipo
di disturbi, per questo motivo si preferisce associare l'informazione ad
altre grandezze meno sensibili al rumore, come la corrente, la frequenza
e l'intervallo di tempo.
Per conseguire questo obiettivo conviene disporre tra monte e valle della
linea di trasmissione dei convertitori VI-IV o Vf-fV o Vt-tV.
Un esempio di convertitore
tensione-corrente è già stato trattato in precedenza assieme ad un esempio
di convertitore corrente-tensione. In questa pagina ci occupiamo dei convertitori
tensione-frequenza.
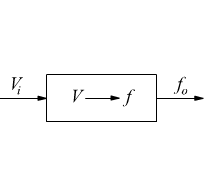
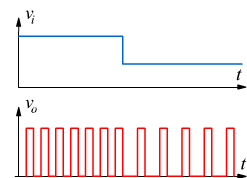
● Il convertitore Tensione-Frequenza: è un dispositivo che fornisce in uscita un segnale che di solito è costituito da una sequenza di impulsi, tutti della stessa ampiezza, la cui frequenza è direttamente proporzionale al valore del segnale di ingresso. Se varia l’ampiezza del segnale di ingresso cambia di conseguenza la frequenza del segnale di uscita.
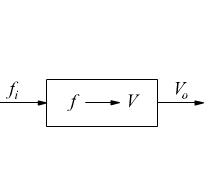
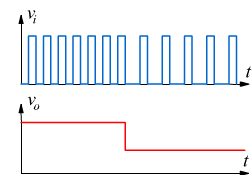
● Il convertitore Frequenza-Tensione: è un dispositivo al cui ingresso è applicata una sequenza regolare di impulsi della stessa ampiezza e che fornisce in uscita una tensione il cui valore è direttamente proporzionale alla frequenza del segnale applicato. Se varia la frequenza del segnale di ingresso cambia di conseguenza l’ampiezza del segnale di uscita.
Spesso lo stesso circuito usato per effettuare la conversione tensione-frequenza può essere utilizzato per fare la conversione frequenza-tensione, semplicemente invertendo alcune connessioni tra i diversi componenti circuitali.
Convertitore tensione-frequenza con BJT
Il circuito è costituito da un integratore invertente collegato a monte di un comparatore a trigger di Schmitt. Per semplicità assumiamo che le tensioni di alimentazione e di saturazione degli operazionali siano uguali: ±Vcc=±Vsat=±15V e che in ingresso venga applicata la tensione costante Vi.
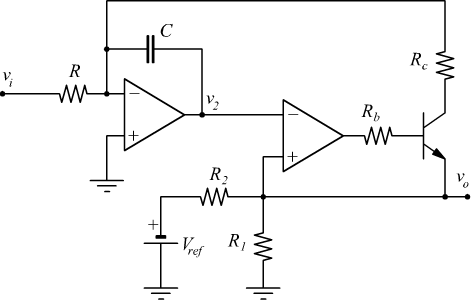
Quando l'uscita del comparatore è pari a -Vcc il BJT è OFF e affinché ciò avvenga è necessario che la tensione in uscita dal comparatore a livello basso (-Vcc) sia inferiore alla tensione sul morsetto non invertente del comparatore. In queste condizioni il segnale in uscita dall'integratore invertente è dato da:
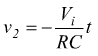 nell'ipotesi
del condensatore scarico. La tensione sul morsetto non invertente del
comparatore è data da
nell'ipotesi
del condensatore scarico. La tensione sul morsetto non invertente del
comparatore è data da
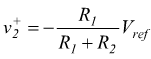
La tensione della rampa diminuisce progressivamente fino a raggiungere la tensione di soglia alla quale si arriva dopo un tempo T1 per il quale è
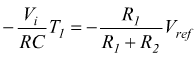 da
cui si ottiene
da
cui si ottiene 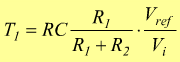
Quando la tensione di uscita del comparatore è +Vcc il BJT è ON; l'equazione delle correnti relative al nodo di massa virtuale dell'integratore è
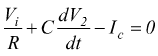
con Ic corrente di collettore del transistor; si ottiene di conseguenza
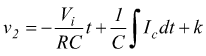
dove il valore della costante k coincide con il valore raggiunto alla fine di T1. Per cui
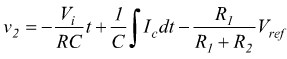
il valore della corrente di collettore può essere trovata come
![]()
Scegliendo valori opportuni si può fare in modo che il BJT conduca, portandosi in saturazione; in queste condizioni la tensione di uscita si porta approssimativamente al potenziale zero e la corrente in R1 diventa trascurabile, dunque

affinché si abbia una condizione di regime occorre che il termine dentro la parentesi sia negativo, in modo da poter produrre una rampa decrescente che ripristini le condizioni iniziali sul condensatore. Si trova in questo modo la condizione che ci assicura un funzionamento corretto cioè:
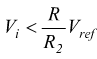
Imponiamo, inoltre, che la tensione V2 dopo un tempo pari a T2 raggiunga lo zero
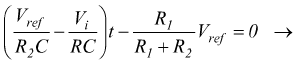
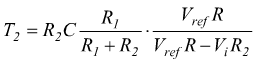
se la condizione che assicura il corretto funzionamento è tale che 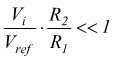
L'equazione di T2 si semplifica ulteriormente e fornisce un valore di T2 che dipende solo dai parametri del circuito e non dalla tensione applicata.
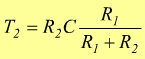
La relazione tra la frequenza f del segnale di uscita e la tensione costante Vi applicata in ingresso è, con queste ipotesi:
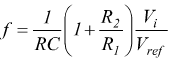
che esprime una proporzionalità diretta tra frequenza e tensione di ingresso. In modo più completo, la relazione può essere espressa anche come:
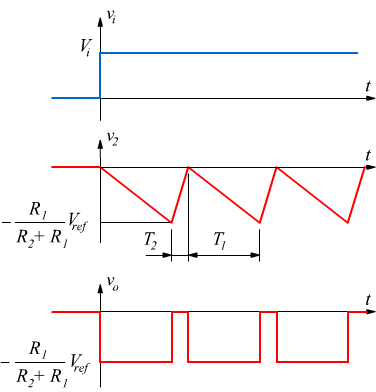
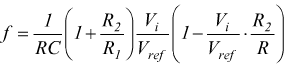 l'andamento
dei segnali è il seguente:
l'andamento
dei segnali è il seguente:
Convertitore tensione-frequenza con JFET
Un convertitore tensione-frequenza può essere realizzato anche tramite un integratore invertente con JFET con a valle un comparatore invertente a trigger di Schmitt. Il JFET serve quando l'uscita v2 dell'integratore è bassa a scaricare la capacità C.
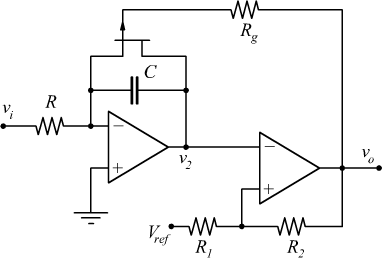
Quando la tensione di uscita v2 dell'integratore è +Vcc il JFET è OFF ed il segnale di uscita dell'integratore invertente è :
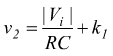
indicando con V2 la tensione raggiunta dalla rampa dopo un tempo pari a T1 e con V1 la tensione iniziale della stessa rampa, l'equazione precedente diventa
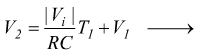
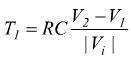 A
A
il comparatore con isteresi, commuta da +Vcc a -Vcc quando la tensione v2 in uscita dall'integratore raggiunge il valore V2 di soglia del comparatore.
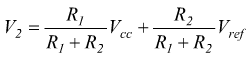
Quando la tensione in uscita all'integratore v2 è -Vcc il JFET è ON; tuttavia, la tensione ai capi del condensatore non può cambiare istantaneamente. Il condensatore si scarica rapidamente attraverso il JFET che conduce con funzionamento in zona attiva; si ha quindi, approssimativamente una rampa che si porta dal valore V2 al valore V1 in corrispondenza del quale si ha una nuova commutazione del comparatore. L'ordine di grandezza della durata T2 di questa rampa, può, in prima approssimazione essere calcolato, considerando che il JFET si trova a condurre con una tensione VGS circa pari a zero; quindi possiamo considerare la IDSS la corrente che lo percorre. Ipotizzando che la IDSS si mantenga costante, l'equazione al nodo invertente dell'integratore è:
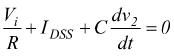
integrando, ricordando che la tensione di ingresso è negativa cioè Vi=-|Vi|
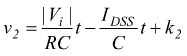
dove la costante di integrazione k2 ha il valore di V2. Affinchè esiste una condizione di regime costante e si ripristini la condizione iniziale, occorre che questa rampa abbia pendenza negativa, cioè |Vi|<R·IDSS . All'istante T2 la tensione v2 in uscita dall'integratore raggiunge il valore V1 di soglia del comparatore dato da
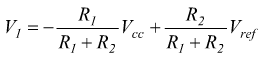 ottenendo
ottenendo 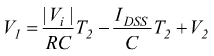 quindi
quindi
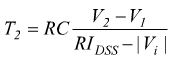 B
B
la differenza V2-V1 rappresenta l'ampiezza del segnale triangolare in uscita dall'integratore; sostituendo la sua espressione nelle formule A e B otteniamo :
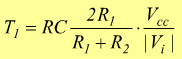 e
e 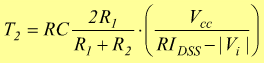
la relazione tra la frequenza del segnale in uscita e la tensione continua in ingresso vale :
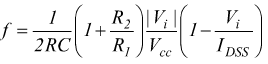 per
Vi<<R·IDSS la formula si semplifica in
per
Vi<<R·IDSS la formula si semplifica in
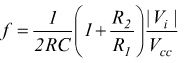

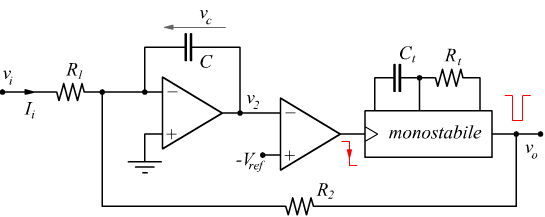
Convertitore tensione-frequenza con monostabile
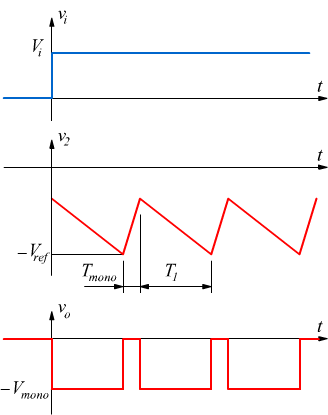
In questo caso il circuito è formato, da un integratore con a valle un comparatore e un dispositivo monostabile.
Facciamo l'ipotesi che il monostabile fornisca, nello stato stabile, una tensione di uscita nulla e, nello stato instabile, un impulso negativo; in queste condizioni all'uscita dell'integratore nello stato stabile si ha:
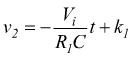
dopo un tempo T1 la tensione di uscita allo stesso avrà subito una variazione pari a
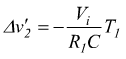 nello
stato instabile avremo
nello
stato instabile avremo 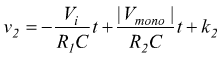
dato che il segnale applicato dal monostabile dura un tempo prefissato, si ottiene una variazione del segnale in uscita all'integratore
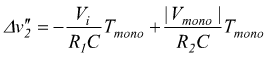
L'esistenza di una condizione di regime impone che il segnale fornito dal monostabile abbia non solo una polarità di segno opposto alla tensione di ingresso (di cui si è già implicitamente tenuto conto nel segno dell'equazione precedente), ma anche un'ampiezza tale da causare una rampa crescente, per cui si deve avere:
 si
ottiene quindi la condizione seguente per un corretto funzionamento
si
ottiene quindi la condizione seguente per un corretto funzionamento
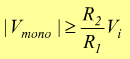 l'andamento
dei segnali è il seguente:
l'andamento
dei segnali è il seguente:
A regime si deve verificare ![]() cioè
cioè
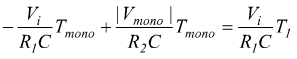
posto 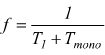 si ricava, allora, la relazione tra segnal di ingresso e frequenza di uscita
si ricava, allora, la relazione tra segnal di ingresso e frequenza di uscita
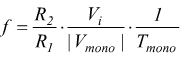
Convertitore frequenza-tensione
E' possibile realizzare un convertitore frequenza-tensione, facendo uso di un semplice integratore approssimato, come schematizzato sotto
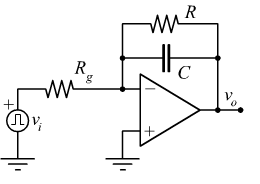
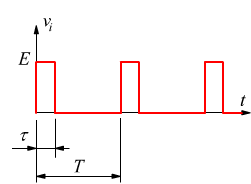
Il segnale di ingresso può essere descritto come
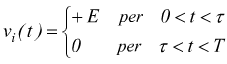
Utilizzando la trasformata di Laplace, il segnale di uscita è dato da
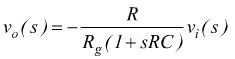
dato che il segnale di ingresso è periodico, la sua trasformata di Laplace vale
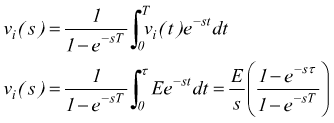
dunque il segnale di uscita diventa
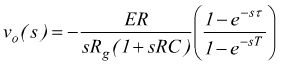
il valore a regime a cui tende il segnale di uscita può essere calcolato col teorema del valor finale (applicando la regola di L'Hospital)
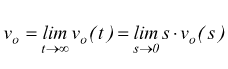


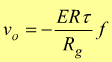
per questo tipo di convertitore dobbiamo ricordarci che la condizione per un corretto funzionamento che si deve avere, è che la frequenza di taglio ft del filtro RC sull'anello di reazione dell'operazionale sia molto minore della frequenza del segnale di ingresso f.
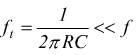
 edutecnica
edutecnica