Tecnica FM
Consiste nel far variare la frequenza della portante proporzionalmente
al valore istantaneo del segnale modulante, lasciandone inalterata l'ampiezza.
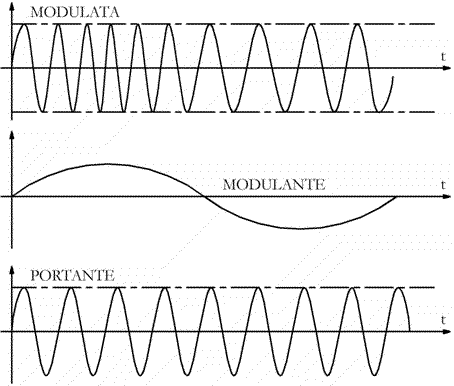
portante
modulante
Per la modulazione di frequenza si dimostra che:
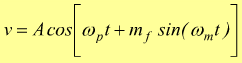modulata inoltre:
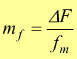indice
di modulazione con
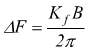
dove Kf è una costante caratteristica del modulatore.
Si può intuire che :
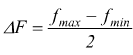intendendo
così, rispetto alla frequenza portante:
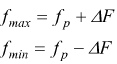Ovviamente
possiamo scrivere: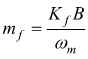 
Ricordiamo per questa tecnica l'espressione della frequenza modulata:
Spettro del segnale FM
La determinazione dello spettro del segnale FM è più elaborata che nel caso del segnale AM. Va considerata la funzione di partenza:
questa forma viene espressa usando le funzioni di Bessel:
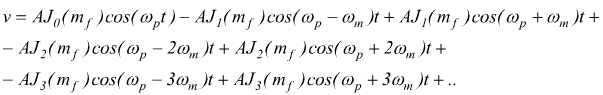
dove le Jn(mf ) sono le funzioni di Bessel (vedi grafico) ;
| mf | Jo | J1 | J2 | J3 | J4 | J5 | J6 | J7 | J8 | J9 | J10 | J11 | J12 | J13 | J14 | J15 | J16 |
|
0
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
0,25
|
0,98
|
0,12
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
0,5
|
0,94
|
0,24
|
0,03
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
1
|
0,77
|
0,44
|
0,11
|
0,02
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
1,5
|
0,51
|
0,56
|
0,23
|
0,06
|
0,01
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
2
|
0,22
|
0,58
|
0,35
|
0,13
|
0,03
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
2,5
|
-0,05
|
0,5
|
0,45
|
0,22
|
0,07
|
0,02
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
3
|
-0,26
|
0,34
|
0,49
|
0,31
|
0,13
|
0,04
|
0,01
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
4
|
-0,4
|
-0,07
|
0,36
|
0,43
|
0,28
|
0,13
|
0,05
|
0,02
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
5
|
-0,18
|
0,33
|
0,05
|
0,36
|
0,39
|
0,26
|
0,13
|
0,05
|
0,02
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
6
|
0,15
|
-0,28
|
-0,24
|
0,11
|
0,36
|
0,36
|
0,25
|
0,13
|
0,06
|
0,02
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
7
|
0,3
|
0
|
-0,3
|
-0,17
|
0,16
|
0,35
|
0,34
|
0,23
|
0,13
|
0,06
|
0,02
|
-
|
-
|
-
|
-
|
-
|
-
|
|
8
|
0,17
|
0,23
|
-0,11
|
-0,29
|
-0,1
|
0,19
|
0,34
|
0,32
|
0,22
|
0,13
|
0,06
|
0,03
|
-
|
-
|
-
|
-
|
-
|
|
9
|
-0,09
|
0,24
|
0,14
|
-0,18
|
-0,27
|
-0,06
|
0,2
|
0,33
|
0,3
|
0,21
|
0,12
|
0,06
|
0,03
|
0,01
|
-
|
-
|
-
|
|
10
|
-0,25
|
0,04
|
0,25
|
0,06
|
-0,22
|
-0.23
|
-0,01
|
0,22
|
0,31
|
0,29
|
0,2
|
0,12
|
0,06
|
0,03
|
0,01
|
-
|
-
|
|
12
|
0,05
|
-0,22
|
-0,08
|
0,2
|
0,18
|
-0,07
|
-0,24
|
-0,17
|
0,05
|
0,23
|
0,3
|
0,27
|
0,2
|
0,12
|
0,07
|
0,03
|
0,01
|
|
15
|
-0,01
|
0,21
|
0,04
|
-0,19
|
-0,12
|
0,13
|
0,21
|
0,03
|
-0,17
|
-0,22
|
-0,09
|
0,1
|
0,24
|
0,28
|
0,25
|
0,18
|
0,12
|
il primo termine (AJ0) è la portante. Le ampiezze della portante e delle altre componenti sono date da A=ampiezza della portante non modulata, per la corrispondente funzione di Bessel (funzione di mf) .
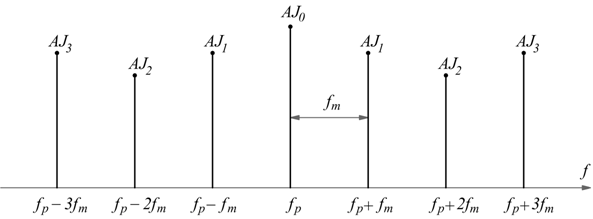
Lo spettro di un segnale FM è dato da infinite coppie di righe simmetriche rispetto la frequenza portante distanti da questa per multipli interi della frequenza modulante (nfm). Si osserva che se mf <<1 solo poche righe sono significative e si parla di segnale FM a banda stretta, mentre mf >>1 se si parla di segnale FM a banda larga. Esiste un numero k che stabilisce il numero significativo di righe spettrali che bisogna considerare:
essendo le righe distanti fm tra loro e simmetriche rispetto la portante, la larghezza di banda:
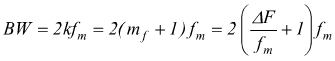
si ottiene così, la regola di Carson:
La potenza di un segnale modulato FM è lo stesso della portante non modulata:
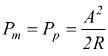dove
R è la resistenza di carico del modulatore.