Teoria dell'informazione
L'informazione è il fattore che diminuisce
l'incertezza sulla conoscenza di un evento.
Le sorgenti di informazioni possono essere analogiche(informazioni continue
nel tempo) oppure discrete (sequenze di simboli).
Se un router appartenente ad una rete telematica, si accorge che una delle tratte a lui collegata, che usualmente è accessibile ed è a veloce percorrenza, risulta ora congestionata o interrotta, si genera una eventualità che viene considerata dal dispositivo un dato ad alto contenuto informativo.
bassa probabilità = elevata informazione
La qualità dell' informazione associata a un evento è funzione dell'inverso delle probabilità che questa eventualità si verifichi.
Considerando una sorgente di informazioni, che emette un determinato
numero di simboli: x1 ,x2 ,…xn ,
(alfabeto) con probabilità di emissione: p1 ,p2 ,…pn
, l'informazione I(xi)
contenuta nell' i-esimo simbolo è funzione di 
.
Si ha:
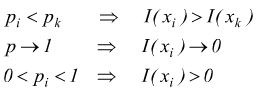
sottintendendo che xk e xi , siano simboli statisticamente indipendenti. la relazione che lega un simbolo xi , alla sua probabilità di emissione pi è:
se la base è 10 l'unita di misura è l'hartley, se la base è 2 l'unita di misura è bit:
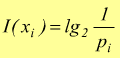
Nel caso di una informazione binaria si può presentare un simbolo che è 0 o 1 con probabilità 0,5 per ciascuno; si ha:
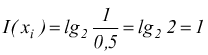[bit]
Il bit è la quantità dell'informazione necessaria e sufficiente a decidere fra due eventi ugualmente probabili e mutuamente esclusivi.
Se una sorgente di segnale può inviare n simboli equiprobabili
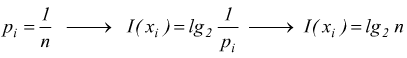
se n=16 si ha 
cioè la sorgente può emettere 16 simboli equiprobabili e l'informazione associata ad ogni simbolo è di 4bit. Se un messaggio è costituito da un numero h di simboli si ha:
la
probabilità che esso si manifesti viene calcolata come:
il
contenuto informativo del messaggio sarà:
Entropia della sorgente
Se una sorgente genera segnali discreti x1,x2,…xn, le cui probabilità sono rispettivamente p1,p2,…pn, il generico i-esimo simbolo è emesso mediamente npi volte per la corrispondente qualità di informazioni risulta:
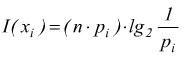
la quantità di informazione totale IT, è uguale alla somma delle singole informazioni degli n simboli è:
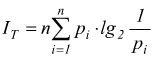
e quindi l'informazione media per simbolo, indicata con H, ottenuta dividendo IT per il numero di simboli n dell'alfabeto della sorgente, risulta:
[
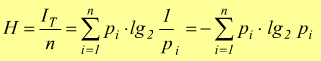bit/simbolo ]
Notiamo come sia H=H(X) dove X={ x1,x2,..,xi,..xn } è l'alfabeto dei simboli. il parametro H, che prende il nome di entropia della sorgente, rappresenta la media pesata delle quantità di informazioni associate ai singoli simboli.
L'Entropia è una misura del contenuto medio di informazione associato ad ognuno dei simboli emessi dalla sorgente, essa viene misurata in bit/simbolo.
Per una sorgente che emette due soli simboli x1 ed x2 aventi probabilità p1 e p2:
come nel caso di un sistema binario x1=0,x2=1 con probabilità p1=p2=0,5.
[bit/simbolo]
Codifica della sorgente
I simboli generati da una sorgente discreta, prima di essere trasmessi vengono opportunamente codificati, cioè a ciascuno viene associato una combinazione univoca di codice (parola) composta da un determinato numero intero l di unità di codice ( lunghezza del codice ).
Per codificare l'intero alfabeto (A,B,C..Z+SPAZIO=27 simboli)
unità. Dato
che l deve essere intero, si pone l=5.
Nel caso in cui volessimo codificare i simboli del display di una calcolatrice avremmo 0,1,2,..9+VIRGOLA=11 simboli
unità
Dato che l deve essere intero, si pone l=4.
| Simboli | Bit1 | Bit2 | Bit3 | Bit4 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| , | 1 | 0 | 1 | 0 |
| Non usate | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 |
In questa codifica è presente una ridondanza
( rappresentata dai simboli non usati ) che può essere diminuita assegnando
ad ogni simbolo combinazioni di codice di lunghezza inversamente proporzionale
alla probabilità di emissione in modo che i simboli a più alta probabilità
di emissione siano formati da un numero di bit inferiore.
La lunghezza media del codice viene definita
come:
senza nessun tipo di codifica di ottimizzazione si ha:
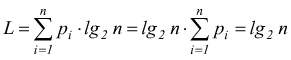
L'efficienza del codice viene definita come
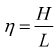
La ridondanza viene definita come
Un codice è definito efficiente quando utilizza un numero di simboli strettamente necessario per codificare l'informazione, si dice, invece, ridondante quando usa un numero di simboli maggiori del necessario. Più un codice è efficiente, tanto minore sarà la sua ridondanza.
In fase di trasmissione intervengono poi altre quantità come il symbol rate ( baud rate )
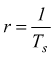[simboli/s]
dove Ts è il tempo impiegato per trasmettere un simbolo e inoltre
l'information rate ( bit rate )
[bit/sec] [Hz]
dove r sono i simboli/s.
Vale inoltre la formula per il calcolo della capacità di canale ( vista anche qui ) che è la massima quantità di informazione che può essere trasmessa nell'unità di tempo sul mezzo trasmissivo.
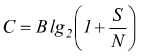[bit/sec] [Hz]
dove B è la banda passante del mezzo trasmissivo e S/N il rapporto segnale/rumore.
Se assumiamo R= C=VTmax è possibile ricavare la banda
necessaria, noto il rapporto S/N.
Algoritmo di Shannon-Fano
a] Gli n simboli dell'alfabeto sorgente vengono ordinati in modo decrescente rispetto alle loro probabilità
b] Si divide l'elenco in due parti in un punto tale che le due parti abbiano approssimativamente la stessa probabilità complessiva.
c] Si assegna il simbolo 0 alla parte alta della lista ed il simbolo 1 alla parte bassa della lista.
d] Si ripetono i due passaggi precedenti fino a ottenere suddivisioni di un solo elemento.
Ad esempio sia data una sorgente di messaggi discreti con un alfabeto formato da 6 simboli:
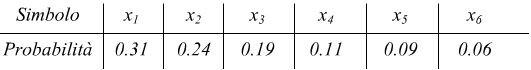
Ordiniamo in modo decrescente in funzione della probabilità di emissione e applichiamo la procedura:
