Premessa
Tenendo conto delle relazioni che legano fra loro i componenti elettrici passivi e le principali grandezze elettriche: tensione e corrente.
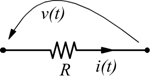
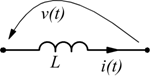
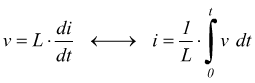
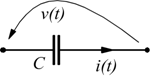
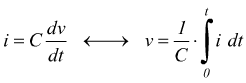
Sia la tensione v=v(t) che la corrente i=i(t) sono considerate funzioni del tempo.
Integratore ideale
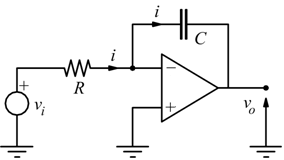
Ipotizziamo un A.O. pilotato all'ingresso invertente da un generatore di segnale con valore istantaneo vi, attraverso la resistenza R, poi chiudiamo l'anello di reazione con un condensatore C.
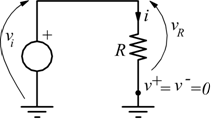
Sulla resistenza R circola la corrente i
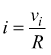
questo perché al morsetto invertente (-) vi sono a 0V (per il principio della massa virtuale).
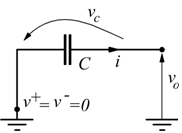
questa corrente viene convogliata sull'anello di reazione e transita sul condensatore; dove risulta
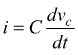
osservando la maglia di uscita risulta essere vc= - vo. Quindi l'equazione precedente può essere riscritta:
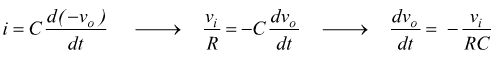
da cui risulta:
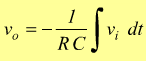
la tensione di uscita è proporzionale all'integrale della tensione di ingresso, il segno meno implica un'inversione di fase rispetto al segnale di ingresso.
Esempio: integrazione di un segnale
sinusoidale
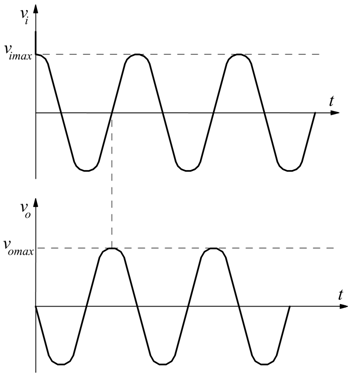
supponiamo che all'ingesso dell'integratore ci sia la tensione 
notando
come il circuito funzioni dome sfasatore in anticipo di 90°.
con K costante arbitraria.
Considerando inizialmente il condensatore scarico vo(0)=0 K=0,perché
sin(0)=0 . Quindi..
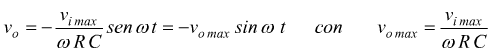
La costante di integrazione può essere diversa se cambiano le condizioni iniziali.
Esempio: integrazione del segnale a gradino
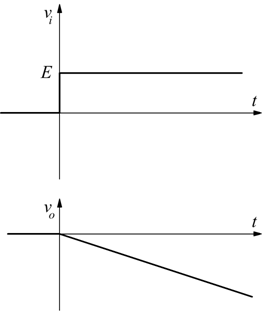
Applicando in ingresso un segnale a gradino (positivo) vi=E,
si ottiene una rampa negativa.
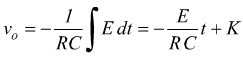
Con K costante arbitraria
La vo per t>0 è assimilabile ad una retta passante per
l'origine con coeff.angolare negativo
considerando inizialmente il condensatore scarico vo(t=0)=0 per cui K=0, quindi:
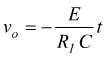
Integratore non invertente
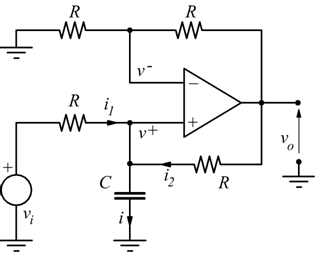
Per costruire un integratore non invertente si può usare uno schema
come quello illustrato.
Il circuito è costituito da quattro resistenze uguali ed un condensatore;
presenta sia reazione negativa che positiva.
Applicando il 1°p.cipio di Kirchoff e il metodo di equipotenzialità degli ingressi al morsetto non invertente si ha:
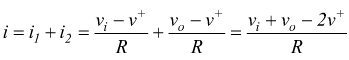ma
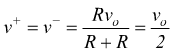quindi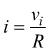 
la tensione ai capi del condensatore è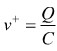 
con
Q=quantità di carica accumulata; per cui:
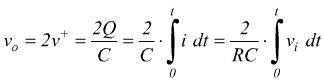
Integratore reale
E' evidente che in un circuito come l'integratore ideale il rischio che
l'A.O. vada in saturazione, a causa di una carica eccessiva del condensatore,
in un senso o nell'altro c'è.
Una soluzione a questo inconveniente consiste nell'introdurre ai capi
del condensatore stesso, una resistenza ausiliaria Rf.
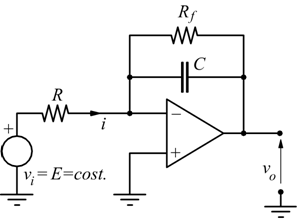
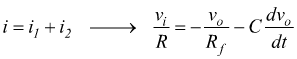
se consideriamo vi=E=costante la precedente è una eq.differenziale a coefficienti costanti, omogenea che fornisce come soluzione:
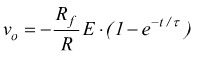con 
Allo stesso risultato si arriverebbe applicando il metodo della trasformata
di Laplace.
Per τ<<t l'andamento della vo può essere approssimato
a quello di una rampa negativa; pertanto il comportamento dell'integratore
reale può essere approssimato a quello ideale.
Derivatore ideale
Ipotizziamo un A.O. pilotato all'ingresso invertente da un generatore di segnale con valore istantaneo vi, in serie ad un condensatore C, poi chiudiamo l'anello di reazione con attraverso la resistenza R
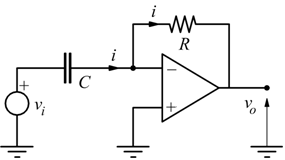
La corrente erogata dal generatore deve valere
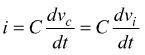
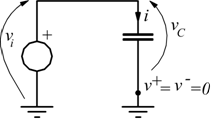
questo perché nella maglia di ingresso è presente solo il generatore vi e il condensatore C (vi=vc).
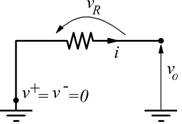
Per lo stesso motivo si osserva che sulla maglia di uscita è presente solo il segnale vo e la c.d.t. vR sulla resistenza; si nota che è
sostituendo la i:
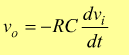
La relazione ottenuta dimostra che la tensione di uscita è proporzionale alla derivata della tensione in ingesso, tramite il fattore moltiplicativo RC; il segno negativo tiene conto dell'inversione di fase.
Esempio: derivazione di un segnale sinusoidale
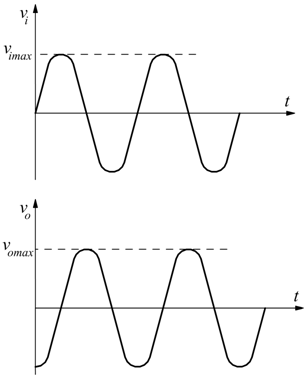
Può essere eseguita la derivazione di un segnale sinusoidale
e si nota come il circuito funzioni dome sfasatore in ritardo di 90°.
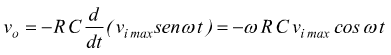
con
Esempio: derivazione del segnale a rampa
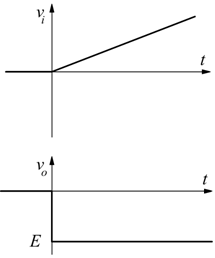
Applicando in ingresso un segnale a rampa
il derivatore fornisce in uscita una tensione negativa a gradino:
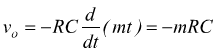
Derivatore non invertente
In questo caso può essere usato il circuito illustrato, che analizzato col metodo della trasformata, ammettendo l'uguaglianza fra le due costanti di tempo R1C1=R2C2.
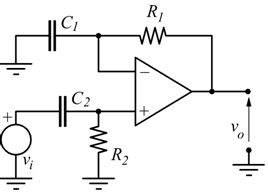
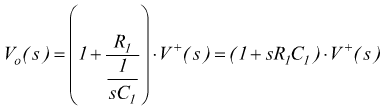
poi si nota
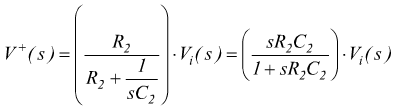
che sostituita nella precedente
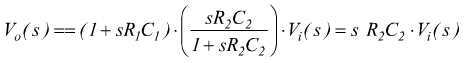
antitrasformando si ottiene la vo(t)
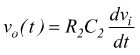
Derivatore reale
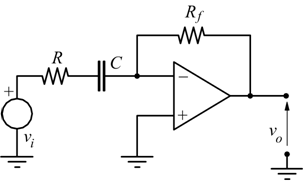
Il maggior inconveniente di un derivatore ideale è la sensibilità
ai disturbi alle alte frequenze, per evitare questo problema si
utilizza normalmente il circuito illustrato.
Trattandosi di un A.O. in config. invertente:
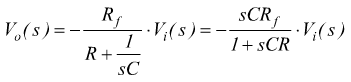
se ipotizziamo che la vi sia una rampa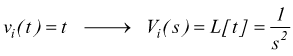 
si avrebbe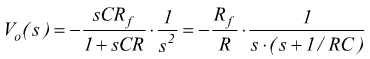 
antitrasformando
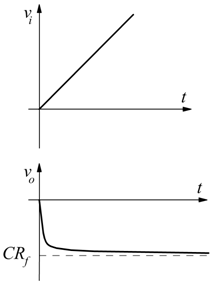
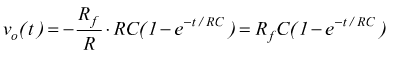
se CRf =1 e il prodotto RC è sufficientemente piccolo l'uscita può essere assimilata ad un gradino di tensione.