DAC: conversione digitale - analogica
Un convertitore digitale-analogico è un dispositivo che riceve in input un numero N decimale codificato in binario, tramite n ingressi e lo rappresenta in uscita in forma analogica.
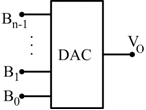
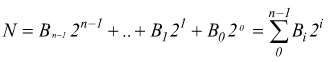
Il principio fondamentale di un DAC è che l'uscita V0 deve essere proporzionale al numero N in ingresso.
![]()
![]() raccogliendo
2n
raccogliendo
2n
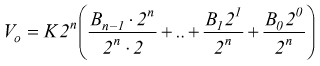
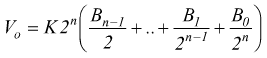 poniamo
poniamo ![]()
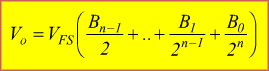
Un convertitore digitale analogico, ad esempio a 4 bit, può essere costruito molto semplicemente con un A.O. , 4 deviatori e 5 resistenze.
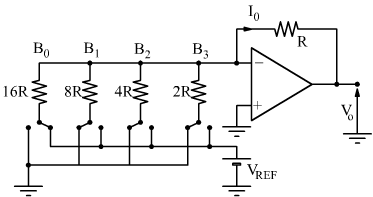
I 4 bit di entrata B0B1B2B3
comandano i 4 deviatori analogici collegati con VREF se il corrispondente
Bi=1 e con la massa se Bi=0.
Le resistenze devono essere dimensionate come indicato, in tal caso il convertitore
viene chiamato a resistori pesati. Se il deviatore è collegato a massa la
tensione ai capi della resistenza è 0 . Se il deviatore è su VREF
nella resistenza circolano correnti che valgono rispettivamente:

Per il principio di sovrapposizione degli effetti:
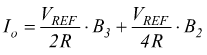
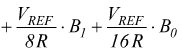
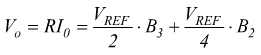
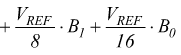 a meno del segno, quindi:
a meno del segno, quindi:
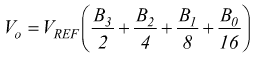
A] Se B0=B1=B2=Bn-1=0 => V0=0
B] Se B1=B2=Bn-1=0 e B0=1 la
V0 è minima 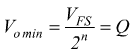
con Q=quanto o passo o risoluzione
del DAC.
C] Il Bit più alto è a 1 Bn-1=1 e tutti gli altri a 0 
D] Se tutti i bit sono a 1
![]()
![]()
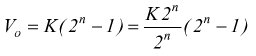
vedi nota:
quindi: 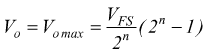
osserviamo che 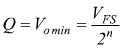 per
cui
per
cui
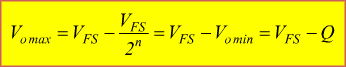
inoltre 
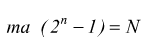
![]()
Quest'ultima formula rimarrà valida anche per gli ADC dove verrà rappresentata
come
![]()
In generale, conviene memorizzare la formula:
![]()
Dove V è la tensione analogica in ingresso al dispositivo nel caso dell'ADC
e in uscita dal dispositivo nel caso del DAC.
N è il numero binario in ingresso ( o uscita).
n è il numero di bit impiegato.
VFS (VREF)è la tensione di fondoscala (di riferimento).
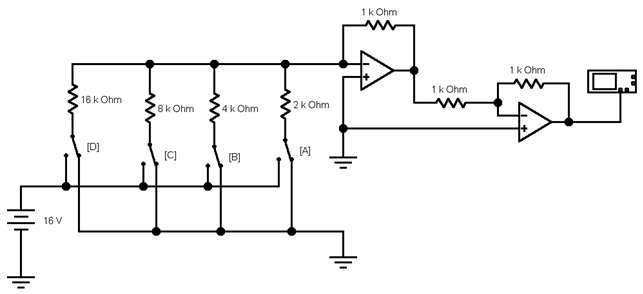
Sotto è riportata una realizzazione con EWB a resistori pesati. Il secondo
operazionale posto in cascata, ha solo lo scopo di invertire il segnale
e renderlo positivo. E' regolato dall'equazione:
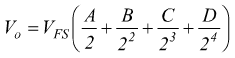
Si nota come ponendo solo il bit più pesante A=1 si ha una Vo=8V
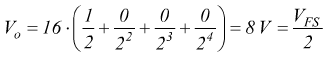
Si nota come ponendo solo il bit meno pesante D=1 si ha una Vo=2,5V

Ponendo tutti i bit a 1 si ha:
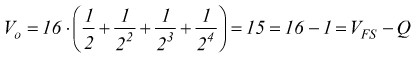
infatti N=(1111)2=(15)10.
Infatti, si dimostra che ![]() in
base alla regola della somma parziale degli elementi di serie geometrica
in ragione 2.
in
base alla regola della somma parziale degli elementi di serie geometrica
in ragione 2.
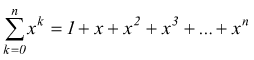 moltiplichiamo
per (1-x)
moltiplichiamo
per (1-x)
![]() semplificando
semplificando
![]()
![]()
![]()
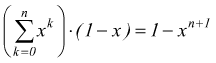 quindi,
quindi,
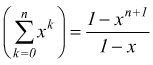 è
stata usata, dunque, la regola
è
stata usata, dunque, la regola
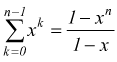 riadattata
alla base 2
riadattata
alla base 2
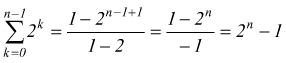
 edutecnica
edutecnica