Amplificatore operazionale : applicazioni lineari
La caratteristica statica di trasferimento (o transcaratteristica) dell' amplificatore operazionale, mette in relazione la tensione di uscita vo con le tensioni di ingresso v+ e v-.
In prima approssimazione, possiamo ritenere che vo dipende dalla
differenza (v+-v-) e non dai valori assoluti assunti
da v+ e v-.
La caratteristica statica vo=f(v+-v-) può
essere rilevata facendo variare lentamente la tensione differenza di ingresso
fra un estremo negativo e un estremo positivo e misurando in corrispondenza
la tensione di uscita. I due estremi (v' e v") entro i quali va contenuta la tensione
differenza, sono in genere precisati dal costruttore e costituiscono il
cosidetto range differenziale del circuito.
La curva presenta un tratto quasi lineare o regione attiva sull'asse vi=(v+-v-)
compreso tra i segnali e v" e v', seguito da due zone di saturazione caratterizzate
dal fatto che la tensione di uscita è insensibile alle variazioni di tensione
differenza all'ingresso.
Nella regione attiva, la caratteristica, può avere una pendenza molto elevata, superiore a 106, poichè i livelli di saturazione +Vsat e -Vsat hanno valori tipici attorno ai 10 V, una variazione v+-v- dell'ordine di una decina di μV è sufficiente per far passare l'amplificatore da un livello di saturazione all'altro. Questa è la ragione principale per cui il punto di lavoro di un A.O. non viene mai fissato vincolando la tensione differenza v+-v-.
Il punto di lavoro di un A.O. è dato (come nel caso del BJT) dall'intersezione tra la caratteristica statica del dispositivo con la rete esterna ad esso. Se volessimo far funzionare l'A.O. semplicemente imponendo con un generatore la differenza v+-v- la situazione che si ottiene mancherebbe di due requisiti fondamentali:
• la prevedibilità, o indipendenza dal particolare campione di un
determinato tipo di A.O;
• la stabilità, o costanza del punto di lavoro nel tempo al variare
dei parametri ambientali, sopratutto della temperatura.
Supponendo di imporre con un generatore la tensione differenziale di ingresso, il punto di lavoro verrebbe fissato, ma basterebbe una leggerissima deriva di offset di tensione di qualche μV per uscire dal range differenziale v"-v' e mandare in saturazione il dispositivo
Il punto di lavoro di un amplificatore operazionale viene di solito fissato con un cammino esterno di reazione negativa.
In questo modo è possibile inclinare la retta di carico con lo scopo di permettere alle due curve di traslare mutuamente senza che il punto di lavoro esca dalla zona attiva per portarsi in saturazione.
La reazione negativa prevede la presenza di un blocco di reazione esterna (B) rispetto al blocco di andata (A) che noi associamo all'amplificatore.
chiamiamo
x : segnale di ingresso
y : segnale di uscita
f : segnale di feedback
d : segnale differenza
Amplificatore operazionale non invertente
Viene introdotto il blocco di reazione costituito dalla rete Rf - Ri indicando con Aol il guadagno ad anello aperto:
se ammettiamo
il guadagno ad anello chiuso dipenderà solo dalla rete esterna all'amplificatore
operazionale (il pedice cl sta a indicare close loop). Se assumiamo che
l'amplificatore sia ideale: con Aol = ∞ e con v+
= v- la dimostrazione di questa formula è ancora più semplice;
in tal caso vi sarà un'unica corrente circolante (i) sulla maglia più esterna
con 
perchè ai
morsetti di ingresso non vi sono correnti entranti (Rin=∞)
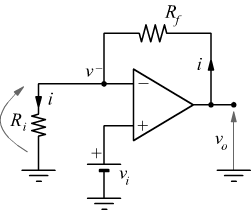
poi dato che v+=v- si riconosce che 
combinando
le due formule
dunque
si ottiene nuovamente 
L'elaborazione eseguita permette di descrivere anche il comportamento della retta di carico che rappresenta il comportamento della rete esterna al dispositivo sul piano ingresso-uscita (vo-vd). Osservando la rete esterna si vede che
quindi
per
Amplificatore operazionale invertente
Questa configurazione è facilmente riconoscibile; è previsto un anello di reazione fra l'uscita vo e l'ingresso invertente costituito dalla resistenza di feedback Rf. L'ingresso non invertente è a massa, il segnale di ingresso è applicato sul lato del morsetto invertente prima della resistenza Ri.
Con questa struttura circuitale la tensione riportata in ingresso è la vRi mentre quella di uscita coincide con la vRf ; risulta allora
il
guadagno ad anello chiuso risulta come nel caso precedente
dove
il segno negativo tiene conto dell'inversione di fase operata dal componente
se 
si
ha 
Infatti, considerando l'operazionale ideale con Aol=∞ e con v+=v- , vi è un'unica corrente circolante sulla rete esterna. Il morsetto v- si troverà (virtualmente) a massa .
cioè 
come si vede la formula del guadagno di un amplificatore operazionale invertente è molto facile da ricordare.
Inseguitore di tensione (voltage follower)
Questo dispositivo anche chiamato buffer non invertente, risolve un inconveniente piuttosto frequente in elettronica che consiste nell' attenuazione che nasce fra due circuiti uno a monte con elevata resistenza d'uscita, l'altro (il carico) a valle con ridotta resistenza di ingresso. occorre generalmente introdurre un circuito "buffer" che funzioni come adattatore di impendenza eliminando il problema suddetto .
Il circuito rappresentato, risponde a questa esigenza: esso infatti presenta un guadagno unitario, elevatissima resistenza di ingresso e bassissima resistenza di uscita. Si può determinare facilmente il guadagno Av considerando che, grazie al corto circuito virtuale la tensione vo coincide con v+ ed è uguale a v- ; dal momento che v- è collegato direttamente all' uscita si a evidentemente vo=vi ; cioè Acl=1. L'inseguitore di tensione viene, dunque, usato per disaccoppiare due circuiti tra loro, in modo che quello a monte non risenta dell'influenza di quello a valle e viceversa.
Impedenze di ingresso e di uscita
Il funzionamento ad anello chiuso dell'A.O. introduce dei vantaggi anche nel caso delle resistenze di ingresso e di uscita.
Nell'A.O. non invertente l'impedenza di ingresso Zi è maggiore dell'impedenza di ingresso propria dell'operazionale ad anello aperto di un fattore (1+AolB) .
Con una reazione negativa l'impedenza di uscita del dispositivo risulterà diminuita dello stesso fattore rispetto al caso in cui non vi sia retroazione.
lo
stesso vantaggio si ottiene nel caso del buffer non invertente.
Tenendo conto che in quel caso Rf=0 ed Ri=∞ → B=1 dunque
Nel caso dell'amplificatore invertente si può invece assumere che
Amplificatore differenziale
In questo caso, siamo in presenza di due segnali di ingresso, uno collocato sul lato invertente e l'altro su quello non invertente.
La relazione fra gli ingressi e l'uscita può essere ottenuta facilmente, applicando il principio di sovrapposizione degli effetti.
Nel primo caso avremo una configurazione non invertente con:
sapendo
che 
si ha 
Nel secondo caso, cortocircuitando v1, Le resistenze R1 ed R2 non sono percorse da corrente, il circuito viene, così a semplificarsi come illustrato e diventa una configurazione invertente.
poi
se le quattro resistenze sono uguali fra loro:
l'amplificatore esegue la differenza fra i due segnali.
Sommatore invertente
Il circuito può prevedere più di un ingresso, noi per semplicità, consideriamo solo due ingressi, anche se potrebbero essere molti di più.
Il modo più semplice per analizzare il circuito è di applicare il principio di sovrapposizione degli effetti.
Nel primo caso si valuta il valore dell'uscita v'o , facendo funzionare solo il generatore v1 e cortocircuitando il generatore v2. Notiamo, in tal caso, che la resistenza R2, è percorsa da una corrente i2=0, dato che la resistenza si trova collocata fra la massa e il morsetto v- che per il principio della massa virtuale si trova a 0V (v-=v+=0).
Tale resistenza può essere dunque ignorata e tolta dal circuito. In questo caso, avremo una configurazione puramente invertente che risponde:
Lo stesso discorso possiamo fare nel secondo caso, quando, valutiamo la risposta in uscita v"o ottenuta facendo funzionare v2, cortocircuitando v1.
dunque
se R1=R2=Rf si avrà
il dispositivo esegue la somma delle tensioni in ingresso e la inverte.
Sommatore non invertente
La sua topologia è indicata in figura, noi consideriamo due ingressi, in realtà potrebbero essere in numero qualsiasi.
Anche in questo caso, dobbiamo procedere col principio di sovrapposizione degli effetti, ottenendo le due tensioni parziali v'o facendo funzionare v1 ed annullando v2 e v"o facendo funzionare v2 ed annullando v1.
Nel primo caso, il circuito collegato, al morsetto non invertente, si riduce ad un partitore:
se per la configurazione non invertente vale la relazione
avremo:
se
tutte le resistenze sono uguali v'o=v1 .
applicando lo stesso metodo facendo funzionare solo v2 si avrebbe v"o=v2 .
il dispositivo sommerebbe semplicemente le tensioni in ingresso.