Giochi equi

            

I giochi equi sono un'applicazione del concetto di speranza matematica (valor medio μ di una variabile casuale). Un gioco è equo se alla fine di numerose partite i giocatori antagonisti si trovano, circa, nelle stesse condizioni di partenza, senza eccessive vincite o grandi perdite. Più precisamente riferendoci al concetto di speranza matematica si può affermare:

Un gioco si dice vantaggioso, equo o svantaggioso a secondo che la speranza matematica E(X) risulti maggiore, uguale o minore di zero. In particolare, un gioco si dice equo quando la speranza matematica di ciascun giocatore è nulla.

Ad esempio : Andrea partecipa ad un gioco. Lancia due dadi e se la somma dei punti è almeno 10 vince 6€ se è al massimo 3, vince 9,6€ altrimenti perde. Studiare se in gioco è equo oppure no nei casi che quando perde Andrea debba pagare:

A 1€
B 2,4€
C 4€

la probabilità di fare almeno 10 è 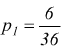    (5+5),(6+6),(4+6),(6+4),(5+6),(6+5)

la probabilità di fare al massimo 3 è 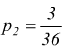  (1+1),(1+2),(2+1)

le probabilità di perdere sono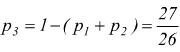 

A se la predita è di 1€ dobbiamo abbiamo la distribuzione

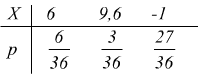    n.b.   

per definizione, la speranza matematica è dunque

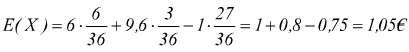
in questo caso il gioco è favorevole (vantaggioso) per Andrea.

B se la perdita è di 2,4€ si ha la distribuzione

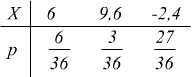
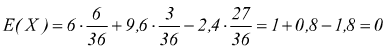
in questo caso il gioco è equo

C se la perdita è di 4€ si ha la distribuzione

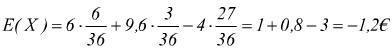
con queste regole il gioco è sfavorevole (svantaggioso)

Caso di due giocatori con due risultati

  

Ipotizziamo un gioco che si svolga tra due giocatori, in tal caso ognuno dei due deposita una somma detta "posta" ed inizia a giocare. Immaginiamo di chiamare s la posta giocata dal primo giocatore che ha p probabilità di vincere. Chiamiamo r la somma depositata dal secondo giocatore che ha q=1-p probabilità di vincere. Studiamo la variabile casuale

X=guadagno del primo giocatore

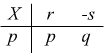
  affinché il gioco sia equo si deve avere E(X)=0

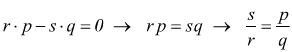
un gioco tra due giocatori è equo se le poste sono proporzionali alle rispettive probabilità di vincita.

Ad esempio : Alfa e Beta giocano con un dado. Alfa vince 4€ se esce un numero divisibile per 3 altrimenti perde 2€. Studiare la variabile casuale

X=guadagno di Alfa

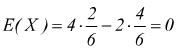 si tratta di un gioco equo, infatti:

   mentre   

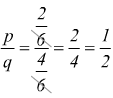
infatti, il rapporto tra le poste è uguale al rapporto tra le probabilità.
In alcuni giochi come le corse dei cavalli si è soliti esprimere le valutazioni di probabilità con il rapporto p/q (odds). Dire che la vittoria di un cavallo è data a a "3 contro 2" significa attribuire la probabilità 3/5 alla vittoria di quel cavallo (p=3, q=2 considerando p+q=5).

Giochi organizzati

        

Nei giochi organizzati, come totocalcio, lotto, enalotto, superenalotto e vari giochi del casinò, per aver diritto di partecipare i paga una somma prima di iniziare il gioco, quindi le eventuali vincite sono "vincite lorde" se chiamiamo S₁ S₂ ...S_n le eventuali vincite lorde ed S il prezzo da pagare per partecipare al gioco, possiamo valutare la variabile aleatoria

X=guadagno del giocatore

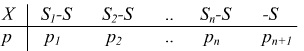
il gioco sarà equo se la speranza matematica è nulla

da cui

essendo   si ha   

si deduce che il prezzo da pagare per partecipare ad un gioco equo organizzato è pari alla speranza matematica della vincita lorda.

Nei giochi organizzati, l'organizzazione fa pagare un "prezzo di partecipazione" molto superiore a quello che si dovrebbe considerare per un gioco equo e questo per alcuni semplici motivi:

● l'organizzazione deve tutelarsi da eventuali perdite dovute al fatto che la frequenza degli eventi risulta diversa dalla probabilità teorica
● deve coprire le spese sostenute per l'organizzazione del gioco
● deve ottenere un guadagno dal gioco

Questa ultima relazione scritta non viene usata solo per giochi o lotterie ma anche per il calcolo dei premi delle varie forme di assicurazione , e anche in questo caso, il valore di S viene opportunamente maggiorato per garantire alla società di assicurazione un guadagno e una tutela in caso di perdite.

Ad esempio : In un gioco organizzato, i giocatori per partecipare devono pagare 1€ si estrae una carta da un mazzo da 40. Si vincono 5€ se è un asso, si vincono 1,5€ se la carta è pari. Si chiede se il gioco sia equo, in caso contrario, si chiede come dovrebbe essere modificata la posta per renderlo equo. Calcolare i guadagno teorico dell'organizzatore su 200 partite. Indichiamo con

X=guadagno dei giocatori

si ha lo schema

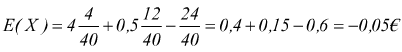
il gioco non è equo ma sfavorevole ai giocatori per avere un gioco equo si dovrebbe rispettare la formula

per avere un gioco equo si dovrebbe pagare una posta di 0,95€.
Su 200 partite l'organizzatore del gioco guadagna teoricamente