La differenza tra moto uniforme e moto uniformemente accelerato genera sempre un poco di confusione nell'interpretazione dei problemi fisici. Molto brevemente si può dire che il moto uniforme è quello che si svolge a velocità costante, mentre il moto uniformemente accelerato si compie ad accelerazione costante (con velocità in aumento o in diminuzione); con tutte le implicazioni che ne conseguono. Infatti, in quest'ultimo caso, si può avere una accelerazione o una decelerazione. Ricordiamoci sempre che nel caso un corpo stia accelerando il vettore accelerazione ha lo stesso verso del vettore velocità. Nel caso il moto sia decelerato , il vettore accelerazione ha verso opposto al vettore velocità, e questo ha certe conseguenze, in particolare sulla forza di inerzia a cui è soggetto il corpo in movimento.
Dal punto di vista cinematico, abbiamo riportato diverse pagine con esercizi su questo argomento, anche se talvolta risulta difficoltoso l'approccio intuitivo a questi concetti.
In questa pagina cerchiamo di rendere visualmente un esempio tradizionale, che è quello del lancio di un proiettile da un aereoplano in movimento. L'esempio è del tutto analogo all'esercizio 20 del moto bidimensionale.
In quel caso, tutta l'attenzione era rivolta al moto del proiettile, che cade per gravità, dunque, il suo moto è accelerato (di valore g=9,81m/s2) lungo la direzione verticale y; mentre la sua velocità è costante lungo la direzione orizzontale x. Questo è dovuto al fatto che in direzione orizzontale, sul proiettile sganciato, non agisce alcuna forza, mentre in direzione verticale agisce la forza di gravità : dove c'è una forza c'è una accelerazione (F=m·a).
Le formule che definiscono le velocità istantanee del moto del proiettile sono note :

con vox velocità iniziale all'istante t=0 in direzione orizzontale x. Queste equazioni portano ben presto alla definizione delle leggi orarie del proiettile.

con h, altezza dell'aereo rispetto al suolo. In queste formule voy=0
perchè la velocità iniziale del proiettile in direzione verticale y, è nulla.
Il tempo impiegato dal proiettile per toccare il suolo si trova ponendo
y=0, dunque:
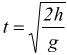
Nel frattempo, si presume che l'aereo proceda in direzione orizzontale
alla stessa velocità costante vox che caratterizza il moto del
proiettile.
Ma se questo non fosse vero e se ad esempio si ipotizasse la presenza di
una accelerazione per esso.
La legge oraria in direzione x per l'aereo sarebbe:
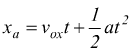
La distanza supplementare percorsa dall'aereo rispetto al proiettile nell'intervallo di tempo in cui quest'ultimo impiega per toccare il suolo sarebbe:

Nell'esempio riportato si cerca di evidenziare questo fatto rappresentando anche la differenza delle traiettorie dei corpi nei due casi.
 edutecnica
edutecnica