Divisione tra due polinomi      

Indichiamo con A e B due polinomi ordinati rispetto alla stessa lettera, col grado di A uguale o maggiore a quello di B (rispetto a quella lettera).
Esisteranno sempre (e sono unici) due polinomi ordinati rispetto alla stessa lettera che noi chiamiamo Q (quoto) ed R (resto).

Il grado di Q è uguale alla differenza tra il grado di A e quello di B, mentre R ha grado minore di B.

Il resto R può anche essere 0 (zero) , in tal caso si ha:

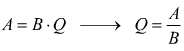
cioè Q è il quoziente esatto tra A e B. In tal caso si dice che A è divisibile per B.
Supponiamo di eseguire la seguente divisione:

1] si ordinano i due polinomi secondo le potenze decrescenti della stessa lettera.

2] si divide il primo termine del dividendo per il primo termine del divisore ed il quoziente è il primo termine del polinomio quoziente

3] si moltiplica questo primo quoziente per ciascuno termine del divisore e si sottrae dal dividendo il polinomio prodotto

4] si divide il primo termine di questo resto parziale per il primo termine del divisore e si ottiene così il secondo termine del quoziente

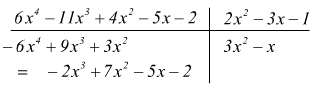
5] si moltiplica questo secondo termine del quoziente per ciascun termine del divisore e si ottiene il polinomio prodotto dal primo resto parziale. Così si ottiene il secondo resto parziale.

6] si divide il primo termine del secondo resto parziale per il primo termine del divisore e si ottiene il terzo termine del quoziente

7] si moltiplica il terzo termine del quoziente per ciascun termine del divisore, si sottrae il polinomio prodotto dal secondo resto parziale e si ottiene il terzo resto parziale.

Poichè il resto è 0, il prodotto del quoziente per il divisore ci dovrà dare il dividendo

Se il polinomio dividendo non è completo, si lascia lo spazio vuoto in corrispondenza dei termini che mancano; nel caso in cui, nello svolgimento della divisione si giunge ad un resto parziale che ha, rispetto alla lettera ordinatrice, un grado inferiore a quello del divisore, non si può procedere oltre; ottenendo così il resto R.