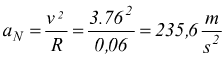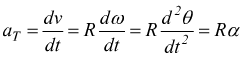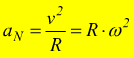Moto Curvilineo
 |
|
 |
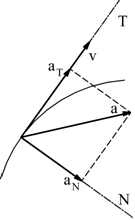
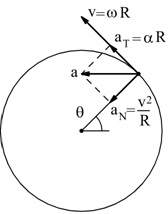
Quando la particella è in moto, il modulo della velocità può cambiare
e questo cambiamento viene riportato dall'accelerazione tangenziale
aT. Quando cambia la direzione della velocità, si ha
una accelerazione normale aN alla traiettoria. |
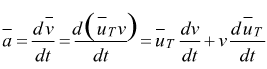
Se il moto fosse rettilineo uT sarebbe costante in intensità
e direzione con 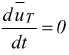 ma
se la traiettoria non è rettilinea la direzione di uT cambia
lungo la stessa, implicando
ma
se la traiettoria non è rettilinea la direzione di uT cambia
lungo la stessa, implicando 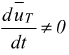 .
.
Con riferimento alla generica traiettoria illustrata sopra:
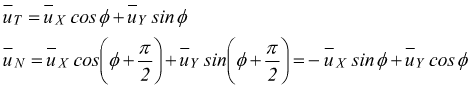
Derivando rispetto al tempo uT:
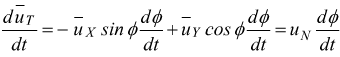
Questo significa che ![]() è
normale alla curva; sapendo che:
è
normale alla curva; sapendo che: 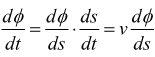
Se ρ=CA è il raggio della curvatura, dalla geometria si ha
![]() per
cui:
per
cui:
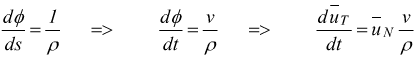
Per il moto curvilineo avremo:
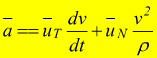
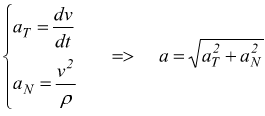
Se il moto curvilineo in esame è uniforme (v=cost.) aT=0 (non
esiste accelerazione tangenziale). Se il moto è rettilineo si ha ρ=∞
e abbiamo aN=0.
Moto circolare
Si ha quando il corpo mobile descrive una traiettoria a forma di circonferenza,
la distanza del mobile dal centro della circonferenza è detto raggio di
rotazione R.
 |
|
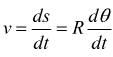 viene
definita, qui, la quantità
viene
definita, qui, la quantità 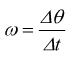 che
in termini di infinitesimi può essere rappresentata come:
che
in termini di infinitesimi può essere rappresentata come:
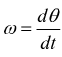
essa viene espressa in [rad/sec] avremo dunque:
![]()
 |
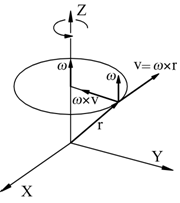
La velocità angolare può essere espressa come quantità vettoriale
la cui direzione è perpendicolare al piano del moto nel senso di
avanzamento di una vite destrorsa che ruoti nel senso di rotazione
del punto mobile. In tal caso la velocità periferica può essere
espressa come il prodotto vettoriale fra la velocità angolare e
il vettore r (distanza fra il punto mobile e il punto O origine
del sistema di riferimento) |
Questa espressione è valida esclusivamente per il moto rotatorio con
r e γ costanti. Notiamo che per il punto C continua a valere la:
![]()
Infatti in tal caso γ=90° e r=R.
Nel moto circolare se ω=cost. si ha il moto
circolare uniforme.
Si tratta di un moto periodico; definiamo:
T=Periodo: tempo per effettuare un giro completo
f=Frequenza: quantità di giri effettuati in un secondo
Se nel tempo t il corpo mobile compie n giri:
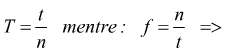
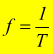
Dalle definizioni date abbiamo:
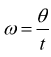 per
un giro completo:
per
un giro completo: 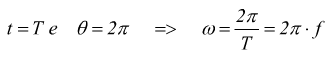
Se il corpo mobile compie n giri in un minuto (rpm) :t=60(sec): e 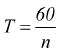 ed
otteniamo:
ed
otteniamo:
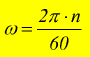 dato
che
dato
che ![]()
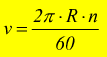
Esempio:
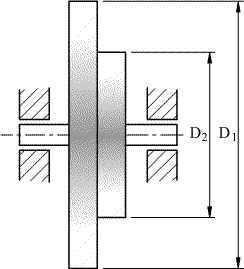
Il cono puleggia in figura compie 300 giri al minuto. Calcolare la sua
velocità angolare in rad/s e la velocità periferica delle due pulegge
che costituiscono il cono Φ1=300mm Φ2=190mm
Φ1=300mm=0,3m
Φ2=190mm=0,19m
 |
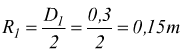 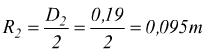 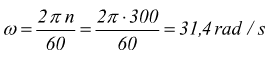 |
Esempio:
Un'auto marcia alla velocità di 108 km/h. Il diametro delle ruote è di
50 cm, quanti giri al minuto compiono?
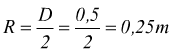
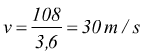
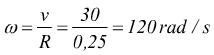
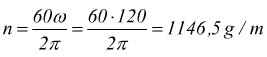
Accelerazione angolare
L'accelerazione angolare è la variazione della velocità angolare nel
tempo.
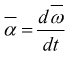
Dato che il moto circolare è piano α ha la stessa direzione di ω
e in modulo:
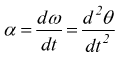
Per conoscere la velocità angolare e l'angolo percorso dal punto mobile
si ha (dall'analisi):
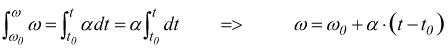
Sostituendo ulteriormente:
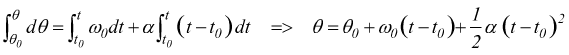
Per il moto puramente circolare combinando la 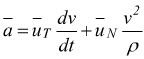 con
la
con
la
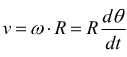 e
con la
e
con la 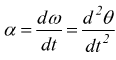
 |
Possiamo ottenere: |
 |
Si osserva come nel moto circolare uniforme (con α=0) non c'è accelerazione tangenziale, ma permane l'accelerazione normale (centripeta) dovuta alla variazione in direzione della velocità. |
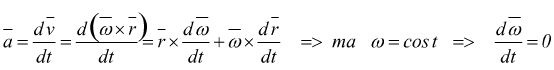
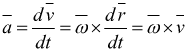 ma
ma
![]() quindi:
quindi:
![]()
Essendo il moto circolare uniforme l'accelerazione ottenuta è quella normale
detta anche accelerazione centripeta.
Esempio:
Calcolare l'accelerazione centripeta di una cinghia trapezoidale, avvolta
su una puleggia di raggio R=60mm, la quale compie 600 g/m.
R=6cm =0,06m
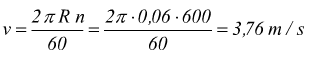 quindi:
quindi: