Equazioni e disequazioni con modulo (con valore assoluto)

Per un numero reale x la definizione di modulo è:

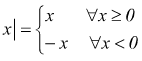
Da questa definizione si deduce che:

In pratica: due numeri reali hanno lo stesso valore assoluto, se sono uguali o se sono opposti.

Valgono le regole:

     e          

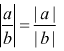
Ad esempio

     impossibile . Dato che il modulo di un numero reale non è mai negativo.

    soddisfatta solo per x=3

        sempre verificata

    sempre verificata eccetto che per    quando x-3=0 , dato che la disequazione 0>0 è falsa x=3 è l'unico valore per il quale non è verificata la disequazione assegnata.

   sempre verificata: il modulo di un numero reale è sempre maggiore o uguale a 0.

   sempre verificata: il modulo di un numero reale è sempre maggiore o uguale a 0 .

   impossibile . Dato che il modulo di un numero reale non è mai negativo.

   sempre verificata tranne che per x=2; in tale circostanza, infatti, il I° membro si annulla del resto la somma di due moduli è sempre positiva, eccetto il caso in cui essi siano simultaneamente nulli.

     sempre verificata perché in questo caso i due moduli non possono essere simultaneamente nulli.

Risulta frequente la risoluzione di disequazioni del tipo:

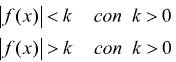
Se k fosse negativo o nullo saremmo già in grado di risolverle, basandoci solo sul concetto di modulo. La prima delle disequazioni date equivale al sistema:

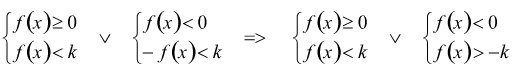
scriveremo:         in pratica avremo:

    riassumendo:

        con         

Attenzione in questo caso la soluzione è l'intersezione delle soluzioni delle due disequazioni.

Per la seconda delle disequazioni assegnate

dato che k è positivo:         riassumendo:

     con      

Attenzione in questo caso la soluzione è l'unione delle soluzioni delle due disequazioni.

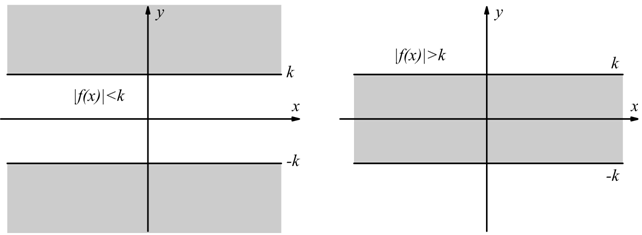
Ad esempio:

    equivale a dire          mettendo a sistema:

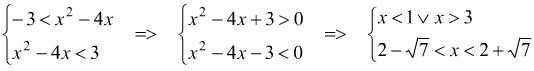
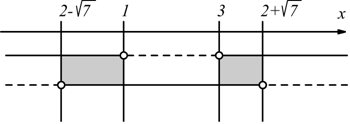
se ne ricava:        intersezione delle soluzioni delle due disequazioni.

Ad esempio:

    equivale a dire      mettendo a sistema:

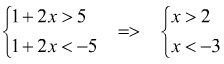
la soluzione è       unione delle soluzioni delle due disequazioni.